这场实在是眼瞎……第三题的题目是检测正方形，我一直在写检测矩形的代码，还认真地排查wa掉的原因，找不到bug甚至怀疑人生……最后还是涛哥火眼金睛发现了我在写判断矩形的代码（我当时已经魔怔了哈哈哈，根本看不到题目2333）。

执行操作后的变量值

题目

存在一种仅支持 4 种操作和 1 个变量 X 的编程语言：

++X 和 X++ 使变量 X 的值加 1
—X 和 X— 使变量 X 的值减 1

最初，X 的值是 0

给你一个字符串数组 operations ，这是由操作组成的一个列表，返回执行所有操作后， X 的最终值。

示例 1：

输入：operations = ["--X","X++","X++"]
输出：1
解释：操作按下述步骤执行：
最初，X = 0
--X：X 减 1 ，X =  0 - 1 = -1
X++：X 加 1 ，X = -1 + 1 =  0
X++：X 加 1 ，X =  0 + 1 =  1

示例 2：

输入：operations = ["++X","++X","X++"]
输出：3
解释：操作按下述步骤执行： 
最初，X = 0
++X：X 加 1 ，X = 0 + 1 = 1
++X：X 加 1 ，X = 1 + 1 = 2
X++：X 加 1 ，X = 2 + 1 = 3

示例 3：

输入：operations = ["X++","++X","--X","X--"]
输出：0
解释：操作按下述步骤执行：
最初，X = 0
X++：X 加 1 ，X = 0 + 1 = 1
++X：X 加 1 ，X = 1 + 1 = 2
--X：X 减 1 ，X = 2 - 1 = 1
X--：X 减 1 ，X = 1 - 1 = 0

提示：

1 2	1 <= operations.length <= 100 operations[i] 将会是 "++X"、"X++"、"--X" 或 "X--"

题解

模拟一下即可

class Solution {
public:
    int finalValueAfterOperations(vector<string>& str) {
        int ans=0;
        for(auto &s:str){
            if(s=="++X"||s=="X++") ans++;
            else if(s=="--X"||s=="X--") ans--;
        }
        return ans;
    }
};

数组美丽值求和

题目

给你一个下标从 0 开始的整数数组 nums 。对于每个下标 i（1 <= i <= nums.length - 2），nums[i] 的美丽值等于：

2，对于所有 0 <= j < i 且 i < k <= nums.length - 1 ，满足 nums[j] < nums[i] < nums[k]
1，如果满足 nums[i - 1] < nums[i] < nums[i + 1] ，且不满足前面的条件
0，如果上述条件全部不满足
返回符合 1 <= i <= nums.length - 2 的所有 nums[i] 的美丽值的总和。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：对于每个符合范围 1 <= i <= 1 的下标 i :

- nums[1] 的美丽值等于 2

示例 2：

输入：nums = [2,4,6,4]
输出：1
解释：对于每个符合范围 1 <= i <= 2 的下标 i :

- nums[1] 的美丽值等于 1
- nums[2] 的美丽值等于 0

示例 3：

输入：nums = [3,2,1]
输出：0
解释：对于每个符合范围 1 <= i <= 1 的下标 i :

- nums[1] 的美丽值等于 0

提示：

1 2	3 <= nums.length <= 10^5 1 <= nums[i] <= 10^5

题解

开辟两个数组l和r，l[i]表示数组从0到i位置所有元素的最大值，r[i]表示数组从n-1到i位置所有元素的最小值，那么对第一个条件的判断就可以直接通过l和r数组完成，复杂度简化到$O(n)$。

class Solution {
public:
    int sumOfBeauties(vector<int>& a) {
        int n=a.size();
        vector<int> l(n,INT_MIN),r(n,INT_MAX);
        for(int i=0;i<n;i++){
            if(i!=0) l[i]=max(l[i],l[i-1]);
            l[i]=max(l[i],a[i]);
        }
        for(int i=n-1;i>=0;i--){
            if(i!=n-1) r[i]=min(r[i],r[i+1]);
            r[i]=min(r[i],a[i]);
        }
        int ans=0;
        for(int i=1;i<=n-2;i++){
            if(a[i]>l[i-1]&&a[i]<r[i+1]) ans+=2;
            else if(a[i]>a[i-1]&&a[i]<a[i+1]) ans++;
        }
        return ans;
    }
};

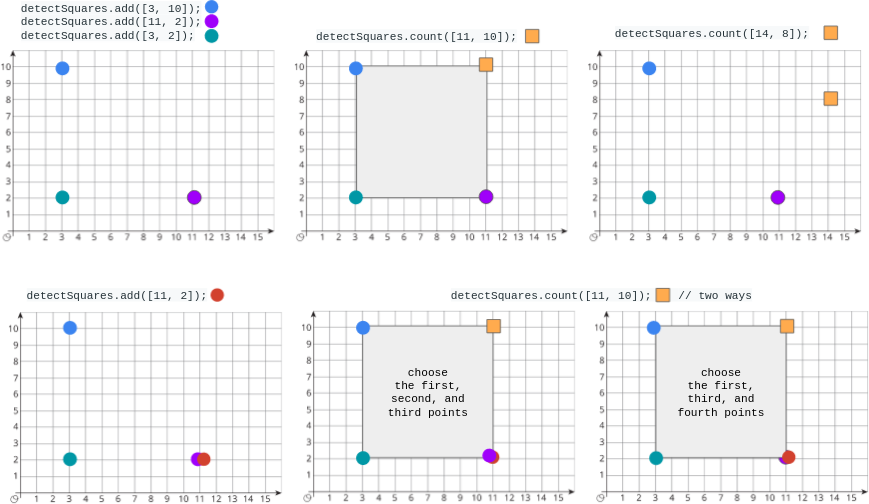
检测正方形

题目

给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法：

添加一个在数据流中的新点到某个数据结构中。可以添加重复的点，并会视作不同的点进行处理。
给你一个查询点，请你从数据结构中选出三个点，使这三个点和查询点一同构成一个面积为正的轴对齐正方形，统计满足该要求的方案数目。
轴对齐正方形是一个正方形，除四条边长度相同外，还满足每条边都与 x-轴或 y-轴平行或垂直。

实现 DetectSquares 类：

DetectSquares() 使用空数据结构初始化对象
void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造轴对齐正方形的方案数。

示例：

输入：
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
输出：
[null, null, null, null, 1, 0, null, 2]

解释：
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择：
                               //   - 第一个，第二个，和第三个点
detectSquares.count([14, 8]);  // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]);    // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择：
                               //   - 第一个，第二个，和第三个点
                               //   - 第一个，第三个，和第四个点

提示：

1
2
3

point.length == 2
0 <= x, y <= 1000
调用 add 和 count 的 总次数 最多为 5000

题解

我人傻了，整了一个小时的判断矩形，疯狂找bug就是找不到，醉了醉了。

正方形的话只需要用map套map存储，key是x坐标，value是一个map，map中存的都是相同x坐标的点的y坐标（因为会有重复的点所以开了一个pair计数，计算x和y都相同的点的数量）。

add的时候只需要将点加入map中即可。

count计数的时候，因为已经确定了一个点，所以先去枚举和这个点x坐标相同的点（遍历mp[p[0]]），这样找到第二个点之后算出距离，再去map中搜索剩下的两个点即可。

class DetectSquares {
public:
    unordered_map<int,unordered_map<int,int>> mp;
    DetectSquares() {
        mp.clear();
    }
    
    void add(vector<int> p) {
        mp[p[0]][p[1]]++;
    }
    
    int count(vector<int> p) {
        int ans=0;
        for(auto& it:mp[p[0]]){
            int y=it.first,num=it.second;
            if(p[1]==y) continue;
            ans+=num*mp[p[0]+abs(y-p[1])][p[1]]*mp[p[0]+abs(y-p[1])][y]+num*mp[p[0]-abs(y-p[1])][p[1]]*mp[p[0]-abs(y-p[1])][y];
        }
        return ans;
    }
};

/**
 * Your DetectSquares object will be instantiated and called as such:
 * DetectSquares* obj = new DetectSquares();
 * obj->add(point);
 * int param_2 = obj->count(point);
 */

重复 K 次的最长子序列

题目

给你一个长度为 n 的字符串 s ，和一个整数 k 。请你找出字符串 s 中重复 k 次的最长子序列。

子序列是由其他字符串删除某些（或不删除）字符派生而来的一个字符串。

如果 seq k 是 s 的一个子序列，其中 seq k 表示一个由 seq 串联 k 次构造的字符串，那么就称 seq 是字符串 s 中一个重复 k 次的子序列。

举个例子，”bba” 是字符串 “bababcba” 中的一个重复 2 次的子序列，因为字符串 “bbabba” 是由 “bba” 串联 2 次构造的，而 “bbabba” 是字符串 “bababcba” 的一个子序列。
返回字符串 s 中重复 k 次的最长子序列。如果存在多个满足的子序列，则返回字典序最大的那个。如果不存在这样的子序列，返回一个空字符串。

示例 1：

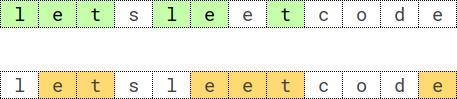
输入：s = "letsleetcode", k = 2
输出："let"
解释：存在两个最长子序列重复 2 次：let" 和 "ete" 。
"let" 是其中字典序最大的一个。

示例 2：

1
2
3

输入：s = "bb", k = 2
输出："b"
解释：重复 2 次的最长子序列是 "b" 。

示例 3：

1
2
3

输入：s = "ab", k = 2
输出：""
解释：不存在重复 2 次的最长子序列。返回空字符串。

示例 4：

1
2
3

输入：s = "bbabbabbbbabaababab", k = 3
输出："bbbb"
解释：在 "bbabbabbbbabaababab" 中重复 3 次的最长子序列是 "bbbb" 。

提示：

n == s.length
2 <= k <= 2000
2 <= n < k * 8
s 由小写英文字母组成

题解

这题坑蛮多的，首先就是这题谜一般的复杂度，很容易让人一看就放弃，然后就是枚举的细节比较多。

首先这道题要重复k次的子序列，最简单的想法就是暴力枚举s串的所有子序列，然后将每个子序列用一个类似于双指针的算法进行暴力匹配，符合条件更新答案，不过这样肯定是会tle的。那么该如何剪枝呢，主要是两方面：

将枚举的范围缩小。由于枚举的子序列必须要出现在s串中k次，那么也就是说如果出现不了k次的字母必然不符合条件，但是这样剪枝还不够完美。继续推，加入最后的答案中出现了”a…a”这样的子序列k次，那么也就是说a这个字母在s串中必须出现2*k次才对。再比如”b…b…b”这样的子序列能匹配k次，那么b这个字母在s串中必须出现3*k次。那么归纳一下，当对整个s串的字母进行哈希统计后，可以将每个元素的哈希值整除k，这样可以大大地减少枚举范围
将判断的次数减少。这一点比较容易想到，这道题的最终目标是要找到最长的且字典序最大的字符串。那么如果dfs去枚举子序列的时候一开始就从最长的且字典序最大的开始，然后一旦找到符合条件的就直接返回最终结果，将很大程度上减少不必要的判断时间，在代码中我是用优先队列自定义排序规则完成的

class Solution {
public:
    int c[30];
    struct node{
        string s;
        bool operator < (const node& a) const {
            if(a.s.length()==this->s.length())
                return s<a.s;
            else return s.length()<a.s.length();
        }
        node(string str):s(str){}
    };
    priority_queue<node> vs;
    string str;
    void dfs(int d,int n){
        if(d==n) {
            vs.push(node(str));
            return;
        }
        for(int i=0;i<26;i++)
            if(c[i]){
                str+=i+'a';
                c[i]--;
                dfs(d+1,n);
                c[i]++;
                str.pop_back();
            }
    }
    int match(string& s,string& p){
        int res=0;
        for(int i=0,j=0;i<s.length();i++){
            if(s[i]==p[j]) j++;
            if(j==p.length()) j=0,res++;
        }
        return res;
    }
    string longestSubsequenceRepeatedK(string s, int k) {
        string ans;
        memset(c,0,sizeof c);
        for(auto& ch:s){
            c[ch-'a']++;
        }
        for(int i=0;i<26;i++) c[i]/=k;
        int mx=0;
        for(int i=7;i>=1;i--){
            str="";
            dfs(0,i);
            while(!vs.empty()){
                string p=vs.top().s;vs.pop();
                int n=p.length(),cnt=match(s,p);
                if(cnt>=k){
                    ans=p;
                    return ans;
                }
            }
        }
        return ans;
    }
};

In The End

Leetcode周赛第259场题解

执行操作后的变量值

题目

题解

数组美丽值求和

题目

题解

检测正方形

题目

题解

重复 K 次的最长子序列

题目

题解