这场的前三题都比较舒服,第四题比较有难度。
反转单词前缀
题目
给你一个下标从 0 开始的字符串 word 和一个字符 ch 。找出 ch 第一次出现的下标 i ,反转 word 中从下标 0 开始、直到下标 i 结束(含下标 i )的那段字符。如果 word 中不存在字符 ch ,则无需进行任何操作。
例如,如果 word = “abcdefd” 且 ch = “d” ,那么你应该 反转 从下标 0 开始、直到下标 3 结束(含下标 3 )。结果字符串将会是 “dcbaefd” 。
返回 结果字符串 。
示例 1:
1
2
3
4
| 输入:word = "abcdefd", ch = "d"
输出:"dcbaefd"
解释:"d" 第一次出现在下标 3 。
反转从下标 0 到下标 3(含下标 3)的这段字符,结果字符串是 "dcbaefd" 。
|
示例 2:
1
2
3
4
| 输入:word = "xyxzxe", ch = "z"
输出:"zxyxxe"
解释:"z" 第一次也是唯一一次出现是在下标 3 。
反转从下标 0 到下标 3(含下标 3)的这段字符,结果字符串是 "zxyxxe" 。
|
示例 3:
1
2
3
4
| 输入:word = "abcd", ch = "z"
输出:"abcd"
解释:"z" 不存在于 word 中。
无需执行反转操作,结果字符串是 "abcd" 。
|
提示:
1
2
3
| 1 <= word.length <= 250
word 由小写英文字母组成
ch 是一个小写英文字母
|
题解
直接做,没问题的!
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
string reversePrefix(string str, char ch) {
int p=0;
for(int i=0;i<str.size();i++)
if(str[i]==ch){
p=i;
break;
}
reverse(str.begin(),str.begin()+p+1);
return str;
}
};
|
可互换矩形的组数
题目
用一个下标从 0 开始的二维整数数组 rectangles 来表示 n 个矩形,其中 rectangles[i] = [widthi, heighti] 表示第 i 个矩形的宽度和高度。
如果两个矩形 i 和 j(i < j)的宽高比相同,则认为这两个矩形 可互换 。更规范的说法是,两个矩形满足 widthi/heighti == widthj/heightj(使用实数除法而非整数除法),则认为这两个矩形 可互换 。
计算并返回 rectangles 中有多少对 可互换 矩形。
示例 1:
1
2
3
4
5
6
7
8
9
10
| 输入:rectangles = [[4,8],[3,6],[10,20],[15,30]]
输出:6
解释:下面按下标(从 0 开始)列出可互换矩形的配对情况:
- 矩形 0 和矩形 1 :4/8 == 3/6
- 矩形 0 和矩形 2 :4/8 == 10/20
- 矩形 0 和矩形 3 :4/8 == 15/30
- 矩形 1 和矩形 2 :3/6 == 10/20
- 矩形 1 和矩形 3 :3/6 == 15/30
- 矩形 2 和矩形 3 :10/20 == 15/30
|
示例 2:
1
2
3
| 输入:rectangles = [[4,5],[7,8]]
输出:0
解释:不存在成对的可互换矩形。
|
提示:
1
2
3
4
| n == rectangles.length
1 <= n <= 10^5
rectangles[i].length == 2
1 <= widthi, heighti <= 10^5
|
题解
用哈希表标记一下即可,也是比较简单
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public:
long long interchangeableRectangles(vector<vector<int>>& rec) {
long long ans=0;
unordered_map<double,int> mp;
for(auto &v:rec){
ans+=mp[(double)v[0]/v[1]];
mp[(double)v[0]/v[1]]++;
}
return ans;
}
};
|
两个回文子序列长度的最大乘积
题目
你一个字符串 s ,请你找到 s 中两个 不相交回文子序列 ,使得它们长度的 乘积最大 。两个子序列在原字符串中如果没有任何相同下标的字符,则它们是 不相交 的。
请你返回两个回文子序列长度可以达到的 最大乘积 。
子序列 指的是从原字符串中删除若干个字符(可以一个也不删除)后,剩余字符不改变顺序而得到的结果。如果一个字符串从前往后读和从后往前读一模一样,那么这个字符串是一个 回文字符串 。
示例 1:
1
2
3
4
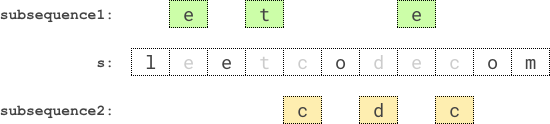
| 输入:s = "leetcodecom"
输出:9
解释:最优方案是选择 "ete" 作为第一个子序列,"cdc" 作为第二个子序列。
它们的乘积为 3 * 3 = 9 。
|
示例 2:
1
2
3
4
| 输入:s = "bb"
输出:1
解释:最优方案为选择 "b" (第一个字符)作为第一个子序列,"b" (第二个字符)作为第二个子序列。
它们的乘积为 1 * 1 = 1 。
|
示例 3:
1
2
3
4
| 输入:s = "accbcaxxcxx"
输出:25
解释:最优方案为选择 "accca" 作为第一个子序列,"xxcxx" 作为第二个子序列。
它们的乘积为 5 * 5 = 25 。
|
提示:
1
2
| 2 <= s.length <= 12
s 只含有小写英文字母。
|
题解
由于长度很小,所以可以直接进行暴搜,字符串每一个位置有三种选择:
- 将其加入第一个子序列
- 将其加入第二个子序列
- 都不加入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
int n,ans;
vector<int> v;
bool judge(string& s){
for(int i=0,j=s.length()-1;i<j;i++,j--){
if(s[i]!=s[j]) return false;
}
return true;
}
void dfs(string& s,string a,string b,int d){
if(d==n){
if(judge(a)&&judge(b))
ans=max(ans,(int)a.length()*(int)b.length());
return;
}
dfs(s,a+s[d],b,d+1);
dfs(s,a,b+s[d],d+1);
dfs(s,a,b,d+1);
}
int maxProduct(string s) {
n=s.length(),ans=0;
string a,b;
dfs(s,a,b,0);
return ans;
}
};
|
每棵子树内缺失的最小基因值
题目
有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ,其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ,所以 parents[0] == -1 。
总共有 105 个基因值,每个基因值都用 闭区间 [1, 10^5] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是节点 i 的基因值,且基因值 互不相同 。
请你返回一个数组 ans ,长度为 n ,其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。
节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。
示例 1:
1
2
3
4
5
6
7
8
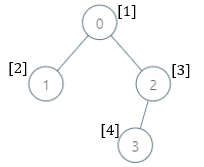
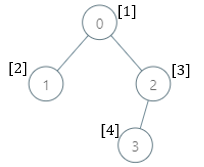
| 输入:parents = , nums =
输出:
解释:每个子树答案计算结果如下:
- 0:子树包含节点 ,基因值分别为 。5 是缺失的最小基因值。
- 1:子树只包含节点 1 ,基因值为 2 。1 是缺失的最小基因值。
- 2:子树包含节点 ,基因值分别为 。1 是缺失的最小基因值。
- 3:子树只包含节点 3 ,基因值为 4 。1是缺失的最小基因值。
|
示例 2:
1
2
3
4
5
6
7
8
9
10
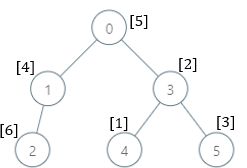
| 输入:parents = , nums =
输出:
解释:每个子树答案计算结果如下:
- 0:子树内包含节点 ,基因值分别为 。7 是缺失的最小基因值。
- 1:子树内包含节点 ,基因值分别为 。 1 是缺失的最小基因值。
- 2:子树内只包含节点 2 ,基因值为 6 。1 是缺失的最小基因值。
- 3:子树内包含节点 ,基因值分别为 。4 是缺失的最小基因值。
- 4:子树内只包含节点 4 ,基因值为 1 。2 是缺失的最小基因值。
- 5:子树内只包含节点 5 ,基因值为 3 。1 是缺失的最小基因值。
|
示例 3:
1
2
3
| 输入:parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
输出:[1,1,1,1,1,1,1]
解释:所有子树都缺失基因值 1 。
|
提示:
1
2
3
4
5
6
7
| n == parents.length == nums.length
2 <= n <= 10^5
对于 i != 0 ,满足 0 <= parents[i] <= n - 1
parents[0] == -1
parents 表示一棵合法的树。
1 <= nums[i] <= 10^5
nums[i] 互不相同。
|
题解
这个超时了2333。
思路是先将含有1的子树判断出来(结果会是一条链),然后对链外的子树进行直接dfs收集,对链内的节点需要进行集合的合并,但是由于合并的复杂度比较高还是超时了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| class Solution {
public:
static const int maxn=1e5+10;
vector<int> ans;
unordered_set<int> s[maxn];
int h[maxn],e[maxn],ne[maxn],need[maxn],idx,n;
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void cat(int u,vector<int>& nums,unordered_set<int>& t){
t.insert(nums[u]);
for(int i=h[u];i!=-1;i=ne[i]){
int v=e[i];
cat(v,nums,t);
}
return;
}
void dfs(int u,vector<int>& nums){
s[u].insert(nums[u]);
for(int i=h[u];i!=-1;i=ne[i]){
int v=e[i];
if(need[u]==1){
dfs(v,nums);
for(auto& it:s[v]) s[u].insert(it);
}
else{
unordered_set<int> t;
cat(v,nums,t);
for(auto& it:t) s[u].insert(it);
}
}
for(int i=1;i<maxn;i++)
if(!s[u].count(i)){
ans[u]=i;
break;
}
return;
}
vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
int root,p=-1;
idx=0,n=parents.size();
ans=vector<int>(n,0);
memset(h,-1,sizeof h);
memset(need,0,sizeof need);
for(int i=0;i<n;i++){
if(nums[i]==1) p=i;
if(parents[i]==-1) root=i;
else add(parents[i],i);
}
if(p==-1){
for(int i=0;i<n;i++)
ans[i]=1;
return ans;
}
for(int i=p;i!=-1;i=parents[i]) need[i]=1;
for(int i=0;i<n;i++)
if(!need[i]) ans[i]=1;
dfs(root,nums);
return ans;
}
};
|



