力扣杯2021秋季编程大赛个人赛题解

来写一波刚结束的力扣秋季编程大赛个人赛的题解

这次力扣杯还算打得还可以吧，至少划进前500很稳…

1.无人机方阵

题目

在 「力扣挑战赛」 开幕式的压轴节目 「无人机方阵」中，每一架无人机展示一种灯光颜色。 无人机方阵通过两种操作进行颜色图案变换：

• 调整无人机的位置布局
• 切换无人机展示的灯光颜色

给定两个大小均为 N*M 的二维数组 source 和 target 表示无人机方阵表演的两种颜色图案，由于无人机切换灯光颜色的耗能很大，请返回从 source 到 target 最少需要多少架无人机切换灯光颜色。

注意： 调整无人机的位置布局时无人机的位置可以随意变动。

示例 1：

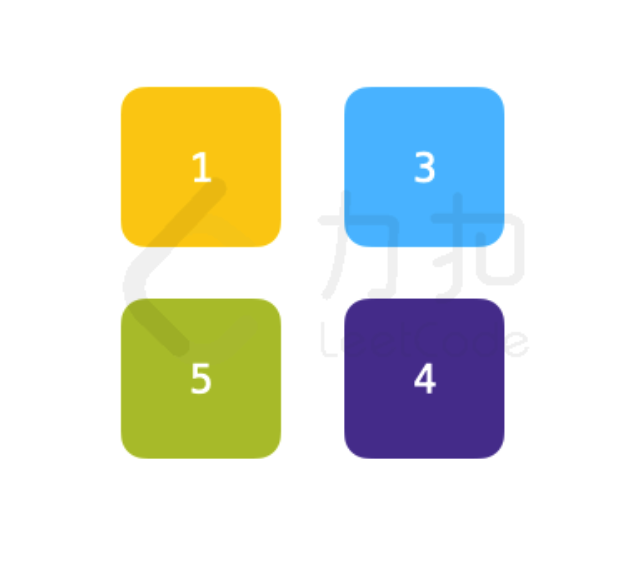
输入：source = [[1,3],[5,4]], target = [[3,1],[6,5]]

输出：1

解释：
最佳方案为
将 [0,1] 处的无人机移动至 [0,0] 处；
将 [0,0] 处的无人机移动至 [0,1] 处；
将 [1,0] 处的无人机移动至 [1,1] 处；
将 [1,1] 处的无人机移动至 [1,0] 处，其灯光颜色切换为颜色编号为 6 的灯光；
因此从source 到 target 所需要的最少灯光切换次数为 1。

示例 2：

输入：source = [[1,2,3],[3,4,5]], target = [[1,3,5],[2,3,4]]

输出：0
解释：
仅需调整无人机的位置布局，便可完成图案切换。因此不需要无人机切换颜色

提示：
n == source.length == target.length
m == source[i].length == target[i].length
1 <= n, m <=100
1 <= source[i][j], target[i][j] <=10^4

题解

首先由于所有的换位都不算次数，所以这题就变得非常水了（完全不需要关心位置，只需要哈希就可以了），将原本的数组和目标数组都哈希一遍，然后遍历目标数组的哈希数组，求个差就行，非常简单

class Solution {
public:
    int minimumSwitchingTimes(vector<vector<int>>& s, vector<vector<int>>& t) {
        vector<int> ss(1e4+10,0);
        vector<int> tt(1e4+10,0);
        for(auto &v:s)
            for(auto &x:v)
                ss[x]++;
        for(auto &v:t)
            for(auto &x:v)
                tt[x]++;
        int ans=0;
        for(int i=1;i<1e4+10;i++)
                if(tt[i]>ss[i])
                    ans+=(tt[i]-ss[i]);
        return ans;
    }
};

2. 心算挑战

题目

「力扣挑战赛」心算项目的挑战比赛中，要求选手从 N 张卡牌中选出 cnt 张卡牌，若这 cnt 张卡牌数字总和为偶数，则选手成绩「有效」且得分为 cnt 张卡牌数字总和。
给定数组 cards 和 cnt，其中 cards[i] 表示第 i 张卡牌上的数字。 请帮参赛选手计算最大的有效得分。若不存在获取有效得分的卡牌方案，则返回 0。

示例 1：

输入：cards = [1,2,8,9], cnt = 3

输出：18

解释：选择数字为 1、8、9 的这三张卡牌，此时可获得最大的有效得分 1+8+9=18。

示例 2：

输入：cards = [3,3,1], cnt = 1

输出：0

解释：不存在获取有效得分的卡牌方案。

提示：

• 1 <= cnt <= cards.length <= 10^5
• 1 <= cards[i] <= 1000

题解

由于最后的答案一定要是偶数，所以如何保证偶数是非常重要的，联想一下曾经学过的一个数学知识：

• 奇数+偶数=奇数
• 偶数+偶数=偶数
• 奇数+奇数=偶数

所以我们不难得出最后答案中一定是包含偶数个奇数的（即奇数必定成对出现），因为如果有奇数个奇数那最后的答案一定是奇数。所以再进行进一步推导，当cnt为奇数时，那么一定不可能所有数都是奇数，一定存在偶数。

立即推当cnt为奇数时答案为sum，那么我们的答案一定可以从cnt-1答案为sum-(最大的偶数)转移过来。换句话说既然cnt一定要取一个偶数，那么一定是取最大的偶数(这个太显然就不解释了)。

所以我们现在将所有cnt为奇数的情况都转化为了cnt为偶数的情况，那么cnt为偶数怎么处理呢，为了保证最后答案是偶数，所以奇数必须成对出现，那么我们干脆就构造两个优先队列，一个只存偶数，一个只存奇数。然后每次拿出偶数优先队列与奇数优先队列顶端的四个数进行比较，奇数的两个大就将两个偶数再插回偶数优先队列，反之亦然，当奇数偶数都不够的情况下说明无解。

class Solution {
public:
    priority_queue<int> odd,even;
    int maxmiumScore(vector<int>& v, int cnt) {
        for(auto& x:v){
            if(x&1) odd.push(x);
            else even.push(x);
        }
        int ans=0;
        if(cnt&1){
            if(even.empty()) return 0;
            else{
                ans+=even.top();
                cnt--;
                even.pop();
            }
        }
        while(cnt){
            if(odd.size()>=2&&even.size()>=2){
                int oa=odd.top();odd.pop();
                int ob=odd.top();odd.pop();
                int ea=even.top();even.pop();
                int eb=even.top();even.pop();
                if(oa+ob>=ea+eb){
                    even.push(ea);
                    even.push(eb);
                    ans+=oa+ob;
                }
                else {
                    odd.push(oa);
                    odd.push(ob);
                    ans+=ea+eb;
                }
            }
            else if(odd.size()>=2){
                int oa=odd.top();odd.pop();
                int ob=odd.top();odd.pop();
                ans+=oa+ob;
            }
            else if(even.size()>=2){
                int ea=even.top();even.pop();
                int eb=even.top();even.pop();
                ans+=ea+eb;
            }
            else return 0;
            cnt-=2;
        }
        return ans;
    }
};

3. 黑白翻转棋

题目

在 n*m 大小的棋盘中，有黑白两种棋子，黑棋记作字母 "X", 白棋记作字母 "O"，空余位置记作 "."。当落下的棋子与其他相同颜色的棋子在行、列或对角线完全包围（中间不存在空白位置）另一种颜色的棋子，则可以翻转这些棋子的颜色。

「力扣挑战赛」黑白翻转棋项目中，将提供给选手一个未形成可翻转棋子的棋盘残局，其状态记作 chessboard。若下一步可放置一枚黑棋，请问选手最多能翻转多少枚白棋。

注意：

• 若翻转白棋成黑棋后，棋盘上仍存在可以翻转的白棋，将可以 继续 翻转白棋
• 输入数据保证初始棋盘状态无可以翻转的棋子且存在空余位置

示例 1：

输入：chessboard = ["....X.","....X.","XOOO..","......","......"]

输出：3

解释：
可以选择下在 [2,4] 处，能够翻转白方三枚棋子。

示例 2：

输入：chessboard = [".X.",".O.","XO."]

输出：2

解释：
可以选择下在 [2,2] 处，能够翻转白方两枚棋子。

示例 3：

输入：chessboard = [".......",".......",".......","X......",".O.....","..O....","....OOX"]

输出：4

解释：
可以选择下在 [6,3] 处，能够翻转白方四枚棋子。

提示：

• 1 <= chessboard.length, chessboard[i].length <= 8
• chessboard[i] 仅包含 "."、"O" 和 "X"

题解

这道题真的调试了N久，很多地方比较细节样例没有覆盖到，所以wa了好几次，苦思冥想终于找到了最终的解法。

其实这道题的思路并不难，由于最多也就8x8的棋盘大小，很容易就将思路定位在搜索上，又由于白子变黑子带来的这种类似于递归的性质，所以很容易想到DFS。

但是这想到DFS很容易，实现起来就麻烦了，我们的DFS需要完成如下几个目标：

• 遍历棋盘，找到空位就开始DFS

• 总共八个方向，先向一个方向猛搜，然后只有搜到黑子后，才可以将路上所有的白子变为黑子

• 路上所有的白子变为黑子后，这些点又会成为新的DFS的起点，开始新的搜索
• 注意地图的保存，每次开始新的空位后要将地图还原

最头痛的起始就是如何先判断有没有黑子在前面，然后在DFS这个操作了，鉴于纯递归比较难写，所以我直接用了一个队列记录沿途的点，如果碰到黑子了那就可以对整个队列里的点进行更新，然后一个个出队开始新的DFS。当然，注意一点就是需要提前将整个队列遍历一遍，将白子修改成黑子，不然如果先DFS下去的话地图上还是白子会出现重复计算（在这wa过一次所以印象深刻）。

class Solution {
public:
    typedef pair<int,int> P;
    int dx[8]={-1,-1,0,1,1,1,0,-1};
    int dy[8]={0,1,1,1,0,-1,-1,-1};
    int n,m,ans=0,res=0;
    void dfs(vector<string>& g,int x,int y){
        for(int i=0;i<8;i++){
            int nx=x+dx[i],ny=y+dy[i];
            queue<P> que;
            while(nx>=0&&nx<n&&ny>=0&&ny<m&&g[nx][ny]=='O'){
                que.push({nx,ny});
                nx+=dx[i],ny+=dy[i];
            }
            if(nx>=0&&nx<n&&ny>=0&&ny<m&&g[nx][ny]=='X'){
                queue<P> t;
                while(!que.empty()){
                    g[que.front().first][que.front().second]='X';
                    t.push({que.front().first,que.front().second});
                    que.pop();
                }
                que=t;
                while(!que.empty()){
                    res++;
                    dfs(g,que.front().first,que.front().second);
                    que.pop();
                }
            }
        }
    }
    int flipChess(vector<string>& g) {
        n=g.size(),m=g[0].size();
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(g[i][j]=='.'){
                    res=0;
                    vector<string> c=g;
                    dfs(c,i,j);
                    ans=max(ans,res);
                }
        return ans;
    }
};

4. 玩具套圈

题目

「力扣挑战赛」场地外，小力组织了一个套玩具的游戏。所有的玩具摆在平地上，toys[i] 以 [xi,yi,ri] 的形式记录了第 i 个玩具的坐标 (xi,yi) 和半径 ri。小扣试玩了一下，他扔了若干个半径均为 r 的圈，circles[j] 记录了第 j 个圈的坐标 (xj,yj)。套圈的规则如下：

• 若一个玩具被某个圈完整覆盖了（即玩具的任意部分均在圈内或者圈上），则该玩具被套中。
• 若一个玩具被多个圈同时套中，最终仅计算为套中一个玩具

请帮助小扣计算，他成功套中了多少玩具。

注意：

• 输入数据保证任意两个玩具的圆心不会重合，但玩具之间可能存在重叠。

示例 1：

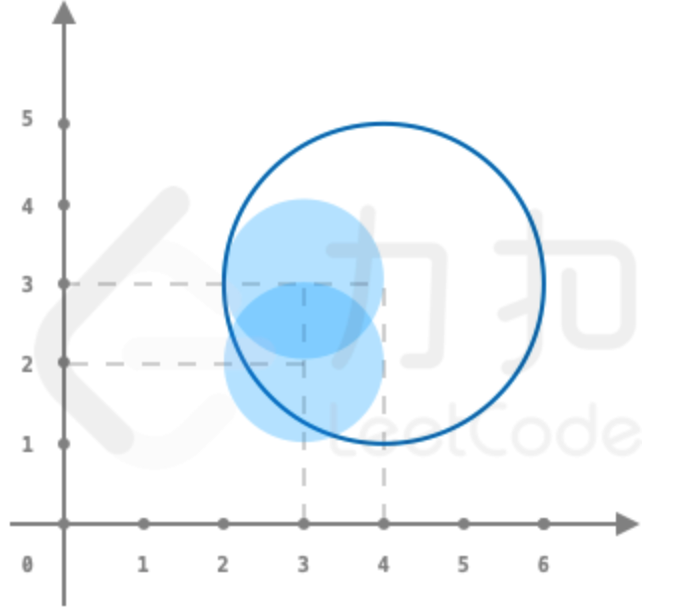
输入：toys = [[3,3,1],[3,2,1]], circles = [[4,3]], r = 2

输出：1

解释： 如图所示，仅套中一个玩具

示例 2：

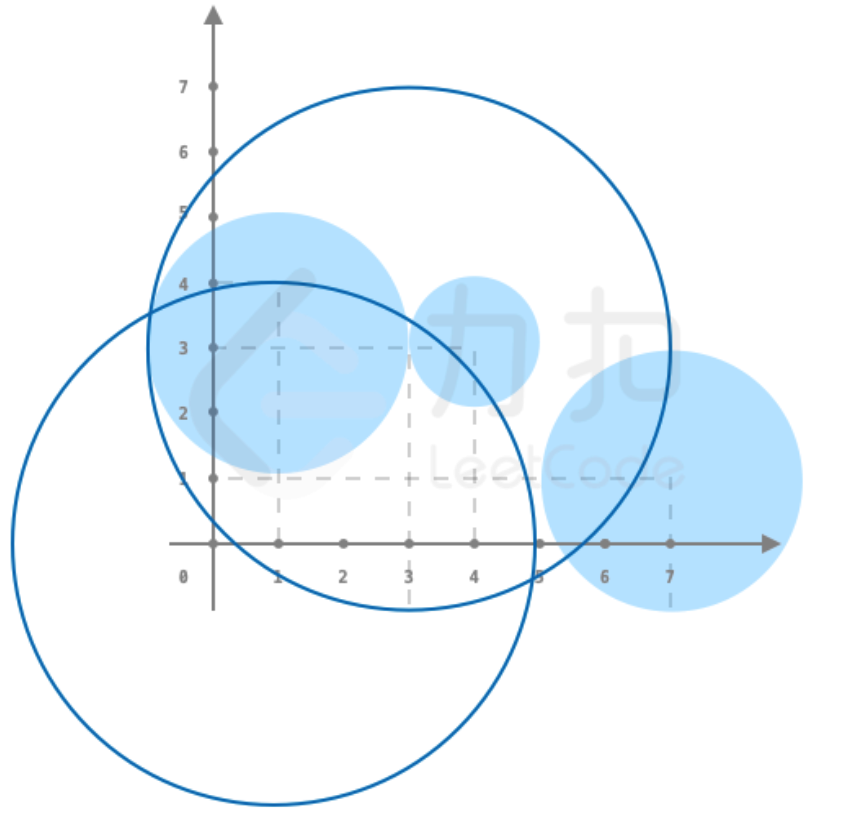
输入：toys = [[1,3,2],[4,3,1],[7,1,2]], circles = [[1,0],[3,3]], r = 4

输出：2

解释： 如图所示，套中两个玩具

提示：

• 1 <= toys.length <= 10^4
• 0 <= toys[i][0], toys[i][1] <= 10^9
• 1 <= circles.length <= 10^4
• 0 <= circles[i][0], circles[i][1] <= 10^9
• 1 <= toys[i][2], r <= 10

题解

首先先放上圆与圆位置关系的定理：

判断依据：设两个圆的半径为R和r，圆心距为d。

则有以下四种关系：

（1）d>R+r 两圆外离； 两圆的圆心距离之和大于两圆的半径之和。

（2）d=R+r 两圆外切； 两圆的圆心距离之和等于两圆的半径之和。

（3）d=R-r 两圆内切； 两圆的圆心距离之和等于两圆的半径之差。

（4）d<R-r 两圆内含；两圆的圆心距离之和小于两圆的半径之差。

（5）d<R+r 两园相交；两圆的圆心距离之和小于两圆的半径之和。

所以这题判断的话只需要让d<=R-r即可也就是代码中的1ll*(x-xi)*(x-xi)+1ll*(y-yi)*(y-yi)<=1ll*(r-ri)*(r-ri)（注：1ll是为了防止溢出将计算过程的类型转成long long）。

刚好套环和玩具都是1e4，如果直接暴力的话$O(n^2)$的算法估计是过不了的，所以需要优化。注意到套环和玩具的半径其实都不大，那么我们可以将套环用map存储（x坐标为键，y坐标为值），然后遍历玩具，每次只需遍历$[xi-r,xi+r]$的范围就可以了（因为r很小所以复杂度很低）。然后确定了x坐标后二分搜索离y坐标最近的两个套环（因为套环大小一样，同一个x坐标的套环，如果y离得近的都套不住，远的就更套不住了）。当x和y都确定后只需要用1ll*(x-xi)*(x-xi)+1ll*(y-yi)*(y-yi)<=1ll*(r-ri)*(r-ri)即可。

当然需要注意玩具半径比套环半径大的话直接continue，这个需要特殊处理，不然会wa！

class Solution {
public:
    int circleGame(vector<vector<int>>& toys, vector<vector<int>>& circles, int r) {
        unordered_map<int,set<int>> mp;
        for(auto& circle:circles)
            mp[circle[0]].insert(circle[1]);
        int ans=0;
        for(auto& toy:toys){
            bool flag=false;
            int xi=toy[0],yi=toy[1],ri=toy[2];
            if(ri>r) continue; //这个很重要
            for(int i=xi-r;i<=xi+r;i++){
                if(!mp.count(i)) continue;
                int x=i;
                auto& s=mp[i];
                auto it=s.lower_bound(yi);
                if(it!=s.end()){
                    int y=*it;
                    if(1ll*(x-xi)*(x-xi)+1ll*(y-yi)*(y-yi)<=1ll*(r-ri)*(r-ri)){
                        flag=true;
                        break;
                    }
                }
                if(it!=s.begin()){
                    it--;
                    int y=*it;
                    if(1ll*(x-xi)*(x-xi)+1ll*(y-yi)*(y-yi)<=1ll*(r-ri)*(r-ri)){
                        flag=true;
                        break;
                    }
                }
            }
            if(flag) ans++;
        }
        return ans;
    }
};

5. 十字路口的交通

题目

前往「力扣挑战赛」场馆的道路上，有一个拥堵的十字路口，该十字路口由两条双向两车道的路交叉构成。由于信号灯故障，交警需要手动指挥拥堵车辆。假定路口没有新的来车且一辆车从一个车道驶入另一个车道所需的时间恰好为一秒钟，长度为 4 的一维字符串数组 directions 中按照 东、南、西、北 顺序记录了四个方向从最靠近路口到最远离路口的车辆计划开往的方向。其中：

• "E" 表示向东行驶；
• "S" 表示向南行驶；
• "W" 表示向西行驶；
• "N" 表示向北行驶。

交警每秒钟只能指挥各个车道距离路口最近的一辆车，且每次指挥需要满足如下规则：

• 同一秒钟内，一个方向的车道只允许驶出一辆车；
• 同一秒钟内，一个方向的车道只允许驶入一辆车；
• 同一秒钟内，车辆的行驶路线不可相交。

请返回最少需要几秒钟，该十字路口等候的车辆才能全部走完。

各个车道驶出的车辆可能的行驶路线如图所示：

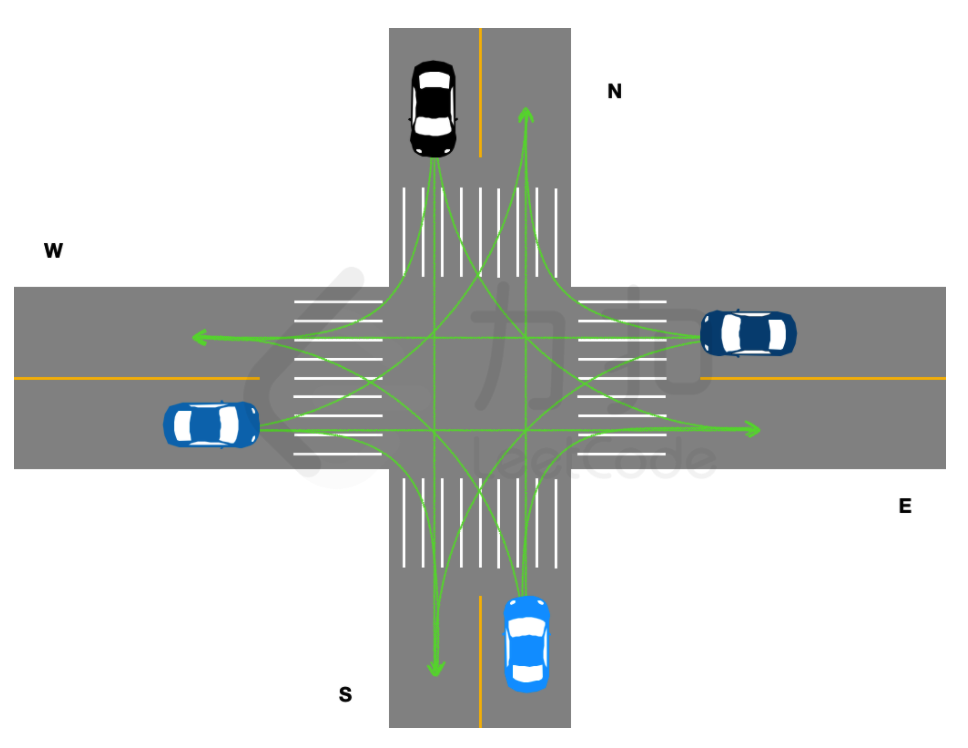
注意：

• 测试数据保证不会出现掉头行驶指令，即某一方向的行驶车辆计划开往的方向不会是当前车辆所在的车道的方向;
• 表示堵塞车辆行驶方向的字符串仅用大写字母 "E"，"N"，"W"，"S" 表示。

示例 1：

输入：directions = ["W","N","ES","W"]

输出：2

解释：
第 1 秒：东西方向排在最前的车先行，剩余车辆状态 ["","N","S","W"]；
第 2 秒：南、西、北方向的车行驶，路口无等待车辆；
因此最少需要 2 秒，返回 2。

示例 2：

输入：directions = ["NS","WE","SE","EW"]

输出：3

解释：
第 1 秒：四个方向排在最前的车均可驶出；
第 2 秒：东南方向的车驶出，剩余车辆状态 ["","","E","W"]；
第 3 秒：西北方向的车驶出。

提示：

• directions.length = 4
• 0 <= directions[i].length <= 20

题解

不会！以后再补！