周赛传送门
https://leetcode-cn.com/contest/weekly-contest-257/
今天的周赛由马化腾AI公司(Pony.ai)赞助!哈哈哈哈!
惊,腾讯老板竟是AI!
开玩笑hhh,老板是楼教主
5863. 统计特殊四元组
题目
给你一个 下标从 0 开始 的整数数组 nums ,返回满足下述条件的 不同 四元组 (a, b, c, d) 的 数目 :
1
| nums[a] + nums[b] + nums[c] == nums[d] ,且a < b < c < d
|
示例 1:
1
2
3
| 输入:nums = [1,2,3,6]
输出:1
解释:满足要求的唯一一个四元组是 (0, 1, 2, 3) 因为 1 + 2 + 3 == 6 。
|
示例 2:
1
2
3
| 输入:nums = [3,3,6,4,5]
输出:0
解释:[3,3,6,4,5] 中不存在满足要求的四元组。
|
示例 3:
1
2
3
4
5
6
7
8
| 输入:nums = [1,1,1,3,5]
输出:4
解释:满足要求的 4 个四元组如下:
- (0, 1, 2, 3): 1 + 1 + 1 == 3
- (0, 1, 3, 4): 1 + 1 + 3 == 5
- (0, 2, 3, 4): 1 + 1 + 3 == 5
- (1, 2, 3, 4): 1 + 1 + 3 == 5
|
提示:
1
2
| 4 <= nums.length <= 50
1 <= nums[i] <= 100
|
题解
四个for暴力
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
int countQuadruplets(vector<int>& nums) {
int n=nums.size(),ans=0;
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++)
for(int k=j+1;k<n;k++)
for(int l=k+1;l<n;l++)
if(nums[i]+nums[j]+nums[k]==nums[l])
ans++;
return ans;
}
};
|
5864. 游戏中弱角色的数量
题目
你正在参加一个多角色游戏,每个角色都有两个主要属性:攻击 和 防御 。给你一个二维整数数组 properties ,其中 properties[i] = [attacki, defensei] 表示游戏中第 i 个角色的属性。
如果存在一个其他角色的攻击和防御等级 都严格高于 该角色的攻击和防御等级,则认为该角色为 弱角色 。更正式地,如果认为角色 i 弱于 存在的另一个角色 j ,那么 attackj > attacki 且 defensej > defensei 。
返回 弱角色 的数量。
示例 1:
1
2
3
| 输入:properties = [[5,5],[6,3],[3,6]]
输出:0
解释:不存在攻击和防御都严格高于其他角色的角色。
|
示例 2:
1
2
3
| 输入:properties = [[2,2],[3,3]]
输出:1
解释:第一个角色是弱角色,因为第二个角色的攻击和防御严格大于该角色。
|
示例 3:
1
2
3
| 输入:properties = [[1,5],[10,4],[4,3]]
输出:1
解释:第三个角色是弱角色,因为第二个角色的攻击和防御严格大于该角色。
|
提示:
1
2
3
| 2 <= properties.length <= 10^5
properties[i].length == 2
1 <= attacki, defensei <= 10^5
|
题解
数组长度是$10^5$,显然$O(n^2)$的算法是过不了的,也就是说无法利用两重循环去判断(如果可以的话这题就是签到题了),所以需要去至少优化一重循环。可以使用pair对组来存储,然后按照first从大到小排序,这样我们可以保证first天然符合条件,只需要考虑second的情况就好了。
但是由于题目中说是需要严格大于,所以first相等的情况我们还是需要考虑的,那么可以使用批处理的方法解决这个问题,一次处理一批first相等的pair,等处理完之后再去更新second的信息,这样就可以保证first相等的情况是不会干扰到我们的答案的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
typedef pair<int,int> P;
int numberOfWeakCharacters(vector<vector<int>>& nums) {
vector<P> v;
for(auto& it:nums) v.push_back({it[0],it[1]});
sort(v.begin(),v.end(),[](P a,P b){
if(a.first==b.first) return a.second>b.second;
else return a.first>b.first;
});
int i=0,mx=-1,ans=0;
while(i<v.size()){
int j=i+1;
while(j<v.size()&&v[j].first==v[i].first) j++;
for(int k=i;k<j&&k<v.size();k++)
if(mx>v[k].second) ans++;
for(int k=i;k<j&&k<v.size();k++)
mx=max(mx,v[k].second);
i=j;
}
return ans;
}
};
|
5865. 访问完所有房间的第一天
题目
你需要访问 n 个房间,房间从 0 到 n - 1 编号。同时,每一天都有一个日期编号,从 0 开始,依天数递增。你每天都会访问一个房间。
最开始的第 0 天,你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 nextVisit 。在接下来的几天中,你访问房间的 次序 将根据下面的 规则 决定:
- 假设某一天,你访问 i 号房间。
- 如果算上本次访问,访问 i 号房间的次数为 奇数 ,那么 第二天 需要访问 nextVisit[i] 所指定的房间,其中 0 <= nextVisit[i] <= i 。
- 如果算上本次访问,访问 i 号房间的次数为 偶数 ,那么 第二天 需要访问 (i + 1) mod n 号房间。
请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大,返回对 109 + 7 取余后的结果。
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:nextVisit = [0,0]
输出:2
解释:
- 第 0 天,你访问房间 0 。访问 0 号房间的总次数为 1 ,次数为奇数。
下一天你需要访问房间的编号是 nextVisit[0] = 0
- 第 1 天,你访问房间 0 。访问 0 号房间的总次数为 2 ,次数为偶数。
下一天你需要访问房间的编号是 (0 + 1) mod 2 = 1
- 第 2 天,你访问房间 1 。这是你第一次完成访问所有房间的那天。
|
示例 2:
1
2
3
4
5
| 输入:nextVisit =
输出:6
解释:
你每天访问房间的次序是 。
第 6 天是你访问完所有房间的第一天。
|
示例 3:
1
2
3
4
5
| 输入:nextVisit = [0,1,2,0]
输出:6
解释:
你每天访问房间的次序是 [0,0,1,1,2,2,3,...] 。
第 6 天是你访问完所有房间的第一天。
|
提示:
1
2
3
| n == nextVisit.length
2 <= n <= 10^5
0 <= nextVisit[i] <= i
|
题解
这题首先需要找一下规律,在纸上模拟一遍流程,当然需要非常注意审题,注意这个条件0 <= nextVisit[i] <= i,这意味着我们的行动路线只会往回跳。
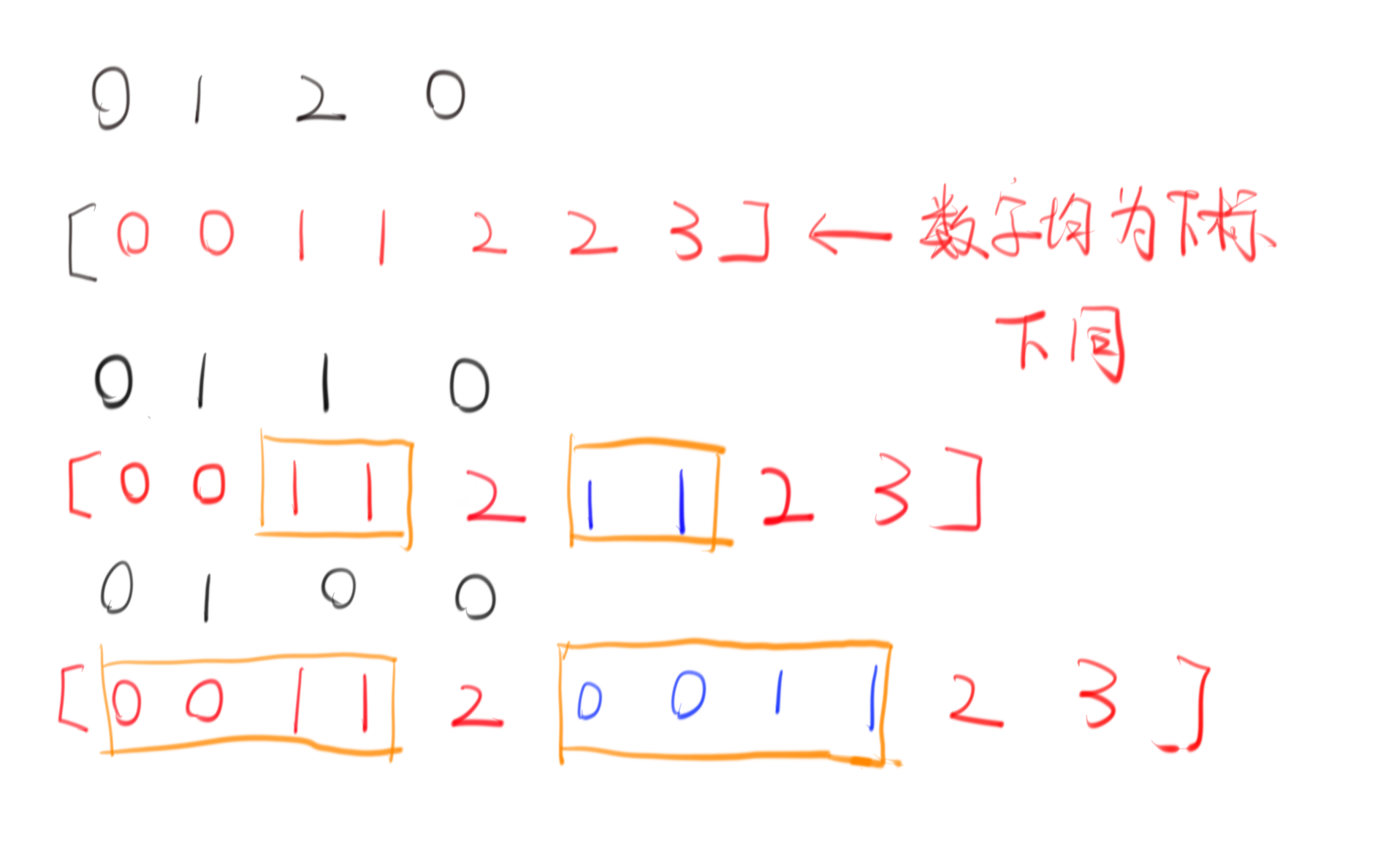
就相当于KMP的模式串根据next数组回溯一样,每次只要nextVisit[i]!=i的话,就会将中间的过程重新来一遍,得出了这一结论后我们开辟一个数组记录从头走到每一个位置的步数的前缀和,然后nextVisit[i]==i就直接+2,nextVisit[i]!=i的话需要去加上s[i-1]-s[nextVisit[i]-1]+2。
注意会爆long long,所以取模的时候先要加上1e9+7,保证一定是正数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
typedef long long ll;
const int mod=1e9+7;
int firstDayBeenInAllRooms(vector<int>& next) {
vector<int> s(next.size()+10,0);
vector<int> t;
t.push_back(0);
for(auto& it:next) t.push_back(it+1);
next=t;
for(auto&it:next) cout << it << ' ';
ll ans=0;
for(int i=1;i<next.size()-1;i++){
if(next[i]==i) ans+=2,s[i]=s[i-1]+2;
else s[i]+=((s[i-1]-s[next[i]-1])%mod+s[i-1])%mod+2,ans+=s[i-1]-s[next[i]-1]+2;
s[i]=(s[i]+mod)%mod,ans=(ans+mod)%mod;
}
return (int)(ans%mod);
}
};
|
5866. 数组的最大公因数排序
题目
给你一个整数数组 nums ,你可以在 nums 上执行下述操作 任意次 :
如果 gcd(nums[i], nums[j]) > 1 ,交换 nums[i] 和 nums[j] 的位置。其中 gcd(nums[i], nums[j]) 是 nums[i] 和 nums[j] 的最大公因数。
如果能使用上述交换方式将 nums 按 非递减顺序 排列,返回 true ;否则,返回 false 。
示例 1:
1
2
3
4
5
6
| 输入:nums = [7,21,3]
输出:true
解释:可以执行下述操作完成对 [7,21,3] 的排序:
- 交换 7 和 21 因为 gcd(7,21) = 7 。nums = [21,7,3]
- 交换 21 和 3 因为 gcd(21,3) = 3 。nums = [3,7,21]
|
示例 2:
1
2
3
| 输入:nums = [5,2,6,2]
输出:false
解释:无法完成排序,因为 5 不能与其他元素交换。
|
示例 3:
1
2
3
4
5
6
7
8
| 输入:nums = [10,5,9,3,15]
输出:true
解释:
可以执行下述操作完成对 [10,5,9,3,15] 的排序:
- 交换 10 和 15 因为 gcd(10,15) = 5 。nums = [15,5,9,3,10]
- 交换 15 和 3 因为 gcd(15,3) = 3 。nums = [3,5,9,15,10]
- 交换 10 和 15 因为 gcd(10,15) = 5 。nums = [3,5,9,10,15]
|
提示:
1
2
| 1 <= nums.length <= 3 * 10^4
2 <= nums[i] <= 10^5
|
题解
第四题不是很难其实。本题的核心就是判断两个元素之间能不能互换的问题,但是由于交换还可以传递,所以这个事情就变得很麻烦。解决这种关系之间传递性的很优秀的数据结构就是并查集,我们可以将拥有相同素数的数合并到一个集合中,这样交换的传递性也可以被保留,最后只要将数组排序一遍判断原来的数字和排序后的数字在不在一个集合内就可以。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
const static int maxn=1e5+10;
int f[maxn];
int find(int x){
return f[x]=x==f[x]?x:find(f[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx!=fy) f[fx]=fy;
}
bool is_same(int x,int y){
return find(x)==find(y);
}
bool gcdSort(vector<int>& nums) {
for(int i=0;i<maxn;i++) f[i]=i;
for(auto n:nums){
int t=n;
for(int i=2;i<=n/i;i++)
if(n%i==0){
merge(i,t);
while(n%i==0) n/=i;
}
if(n>1) merge(n,t);
}
vector<int> sort_nums=nums;
sort(sort_nums.begin(),sort_nums.end());
for(int i=0;i<nums.size();i++){
if(sort_nums[i]!=nums[i]&&!is_same(sort_nums[i],nums[i]))
return false;
}
return true;
}
};
|
