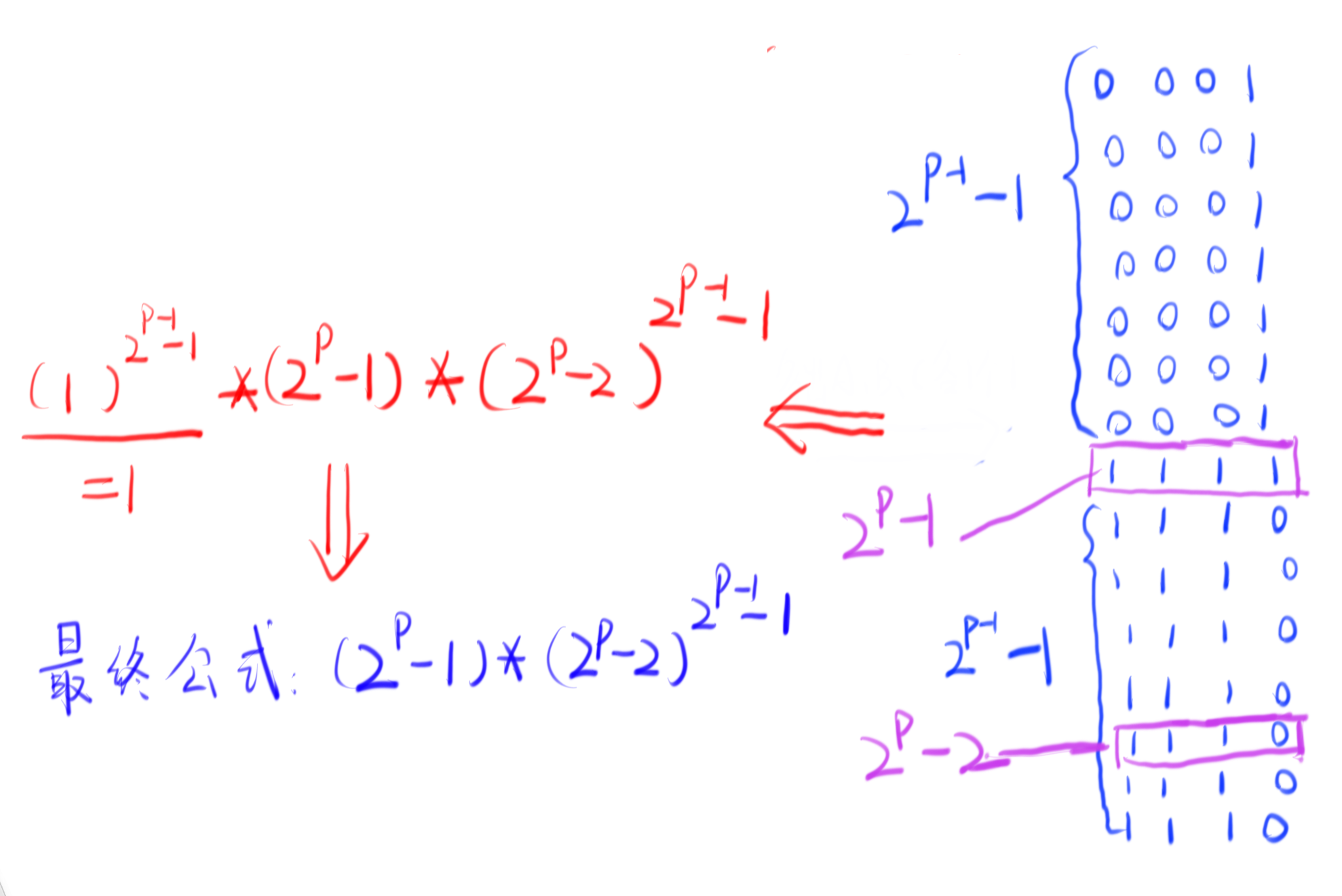周赛传送门
https://leetcode-cn.com/contest/weekly-contest-254/
这场是后来补上的,打了一下虚拟赛,第一题比较简单,第二题大概猜了一下莽过去了,第三题完全没有思路,第四题做了一个多小时,历经一次推倒重写最后过了。
1967. 作为子字符串出现在单词中的字符串数目
题目
给你一个字符串数组 patterns 和一个字符串 word ,统计 patterns 中有多少个字符串是 word 的子字符串。返回字符串数目。
子字符串 是字符串中的一个连续字符序列。
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:patterns = ["a","abc","bc","d"], word = "abc"
输出:3
解释:
- "a" 是 "abc" 的子字符串。
- "abc" 是 "abc" 的子字符串。
- "bc" 是 "abc" 的子字符串。
- "d" 不是 "abc" 的子字符串。
patterns 中有 3 个字符串作为子字符串出现在 word 中。
|
示例 2:
1
2
3
4
5
6
7
8
| 输入:patterns = ["a","b","c"], word = "aaaaabbbbb"
输出:2
解释:
- "a" 是 "aaaaabbbbb" 的子字符串。
- "b" 是 "aaaaabbbbb" 的子字符串。
- "c" 不是 "aaaaabbbbb" 的字符串。
patterns 中有 2 个字符串作为子字符串出现在 word 中。
|
示例 3:
1
2
3
| 输入:patterns = [,,], word =
输出:3
解释:patterns 中的每个字符串都作为子字符串出现在 word 中。
|
提示:
1 <= patterns.length <= 100
1 <= patterns[i].length <= 100
1 <= word.length <= 100
patterns[i] 和 word 由小写英文字母组成
题解
遍历patterns,直接用substr函数暴力比较即可
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
int numOfStrings(vector<string>& v, string s) {
int ans=0;
for(auto& str:v)
for(int i=0;i<s.length();i++)
if(s[i]==str[0]&&s.substr(i,str.length())==str){
ans++;
break;
}
return ans;
}
};
|
1968. 构造元素不等于两相邻元素平均值的数组
题目
给你一个 下标从 0 开始 的数组 nums ,数组由若干 互不相同的 整数组成。你打算重新排列数组中的元素以满足:重排后,数组中的每个元素都 不等于 其两侧相邻元素的 平均值 。
更公式化的说法是,重新排列的数组应当满足这一属性:对于范围 1 <= i < nums.length - 1 中的每个 i ,(nums[i-1] + nums[i+1]) / 2 不等于 nums[i] 均成立 。
返回满足题意的任一重排结果。
示例 1:
1
2
3
4
5
6
| 输入:nums = [1,2,3,4,5]
输出:[1,2,4,5,3]
解释:
i=1, nums[i] = 2, 两相邻元素平均值为 (1+4) / 2 = 2.5
i=2, nums[i] = 4, 两相邻元素平均值为 (2+5) / 2 = 3.5
i=3, nums[i] = 5, 两相邻元素平均值为 (4+3) / 2 = 3.5
|
示例 2:
1
2
3
4
5
6
| 输入:nums = [6,2,0,9,7]
输出:[9,7,6,2,0]
解释:
i=1, nums[i] = 7, 两相邻元素平均值为 (9+6) / 2 = 7.5
i=2, nums[i] = 6, 两相邻元素平均值为 (7+2) / 2 = 4.5
i=3, nums[i] = 2, 两相邻元素平均值为 (6+0) / 2 = 3
|
提示:
3 <= nums.length <= 10^5
0 <= nums[i] <= 10^5
题解
首先我们注意到数组由若干互不相同的整数组成这个先决条件,从这个条件我们可以推出一些有趣的结论:

那么,如果我们可以保证每一个数字的左右两边都大于或者小于自己,这道题也就迎刃而解了,如果进行这样的操作呢?
其实也并不难,只需要进行插值即可,将数组排序后在中间劈开,分为小的那部分和大的那部分,然后大的放一个,小的放一个形成新的数组,具体请看下图来理解:
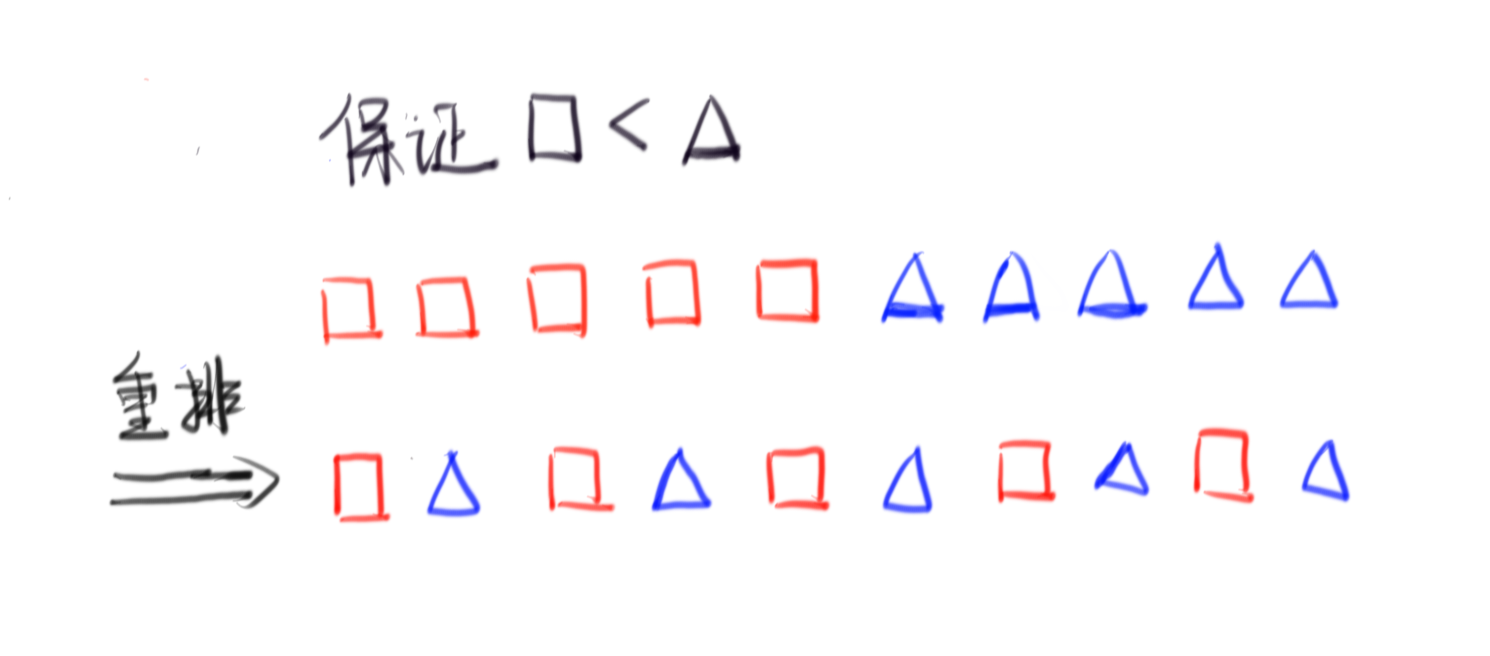
很明显这样就能保证数组符合条件了,当然其实想要优化的话,可以把排序改成快排的划分操作,这样能将复杂度从$O(nlogn)$降为$O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
vector<int> rearrangeArray(vector<int>& nums) {
int n=nums.size()/2;
queue<int> q1,q2;
sort(nums.begin(),nums.end());
for(int i=0;i<=n;i++) q1.push(nums[i]);
for(int i=n+1;i<nums.size();i++) q2.push(nums[i]);
vector<int> ans;
while(!q1.empty()||!q2.empty()){
if(!q1.empty()){
ans.push_back(q1.front());
q1.pop();
}
if(!q2.empty()){
ans.push_back(q2.front());
q2.pop();
}
}
return ans;
}
};
|
1969. 数组元素的最小非零乘积
题目
给你一个正整数 p 。你有一个下标从 1 开始的数组 nums ,这个数组包含范围 [1, 2^p - 1] 内所有整数的二进制形式(两端都 包含)。你可以进行以下操作 任意 次:
从 nums 中选择两个元素 x 和 y 。
选择 x 中的一位与 y 对应位置的位交换。对应位置指的是两个整数 相同位置 的二进制位。
比方说,如果 x = 1101 且 y = 0011 ,交换右边数起第 2 位后,我们得到 x = 1111 和 y = 0001 。
请你算出进行以上操作 任意次 以后,nums 能得到的 最小非零 乘积。将乘积对 10^9 + 7 取余 后返回。
注意:答案应为取余 之前 的最小值。
示例 1:
1
2
3
4
| 输入:p = 1
输出:1
解释:nums = [1] 。
只有一个元素,所以乘积为该元素。
|
示例 2:
1
2
3
4
5
| 输入:p = 2
输出:6
解释:nums = [01, 10, 11] 。
所有交换要么使乘积变为 0 ,要么乘积与初始乘积相同。
所以,数组乘积 1 * 2 * 3 = 6 已经是最小值。
|
示例 3:
1
2
3
4
5
6
7
8
9
| 输入:p = 3
输出:1512
解释:nums = [001, 010, 011, 100, 101, 110, 111]
- 第一次操作中,我们交换第二个和第五个元素最左边的数位。
- 结果数组为 [001, 110, 011, 100, 001, 110, 111] 。
- 第二次操作中,我们交换第三个和第四个元素中间的数位。
- 结果数组为 [001, 110, 001, 110, 001, 110, 111] 。
数组乘积 1 * 6 * 1 * 6 * 1 * 6 * 7 = 1512 是最小乘积。
|
提示:
1 <= p <= 60
题解
如何让相乘的结果最小,首先需要注意的一点就是要相乘的数相互之间的差越大越好,就比如1*5就要比2*3要小。
还有就是,题目中的交换操作并不会改变所有数相加的总和。
明确了这两点,那就来研究一下p=3的情况:
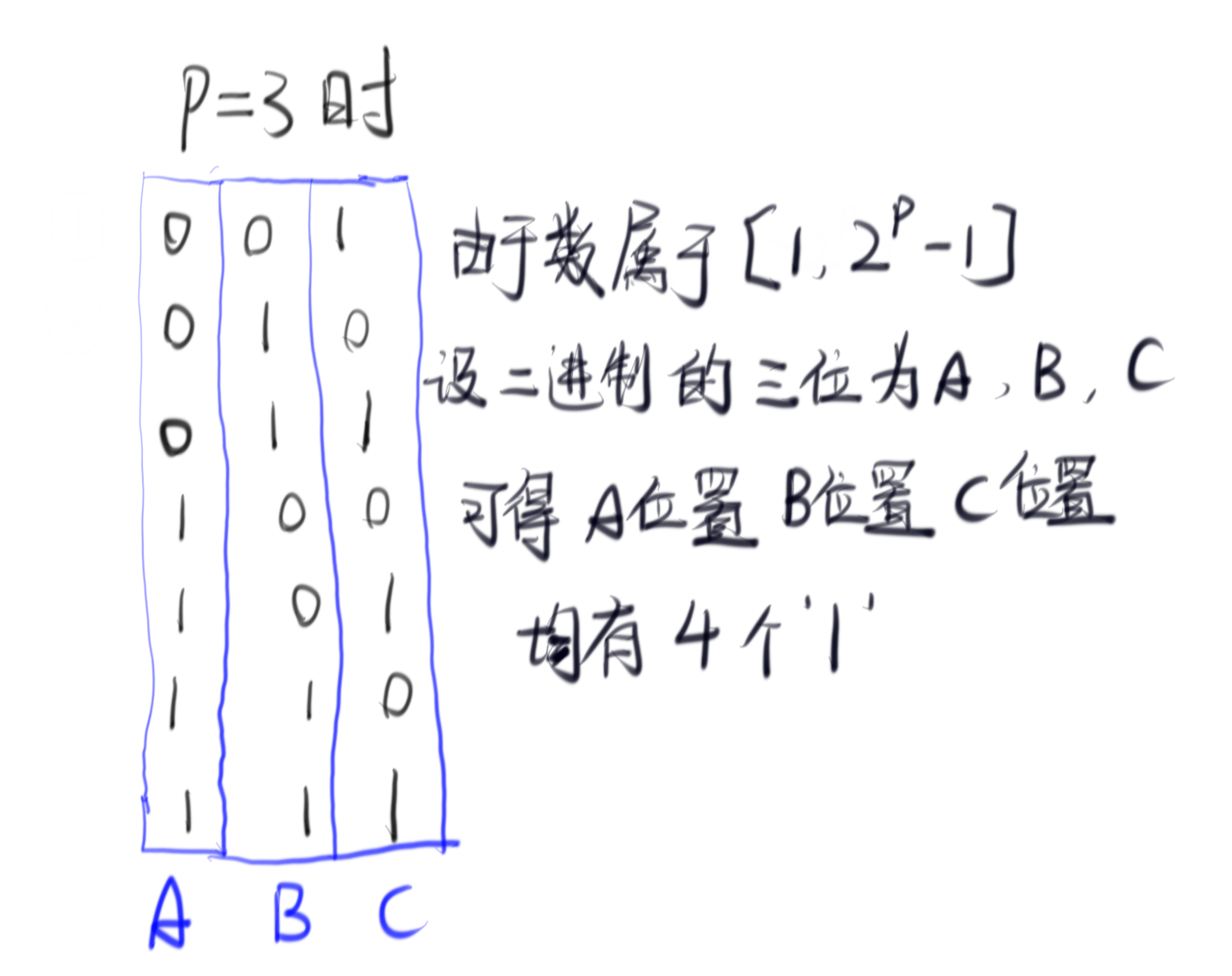
如果设p=4,也可以发现当统计[1,2^p-1]共15个数字的4个二进制位中1的个数是一样的都是8个。
最关键的来了,我们尝试一下转换思路,注意一下题目中说我们可以交换任意次,那么相当于我们是拿着这些1往全是0的矩阵里填!请看下图!
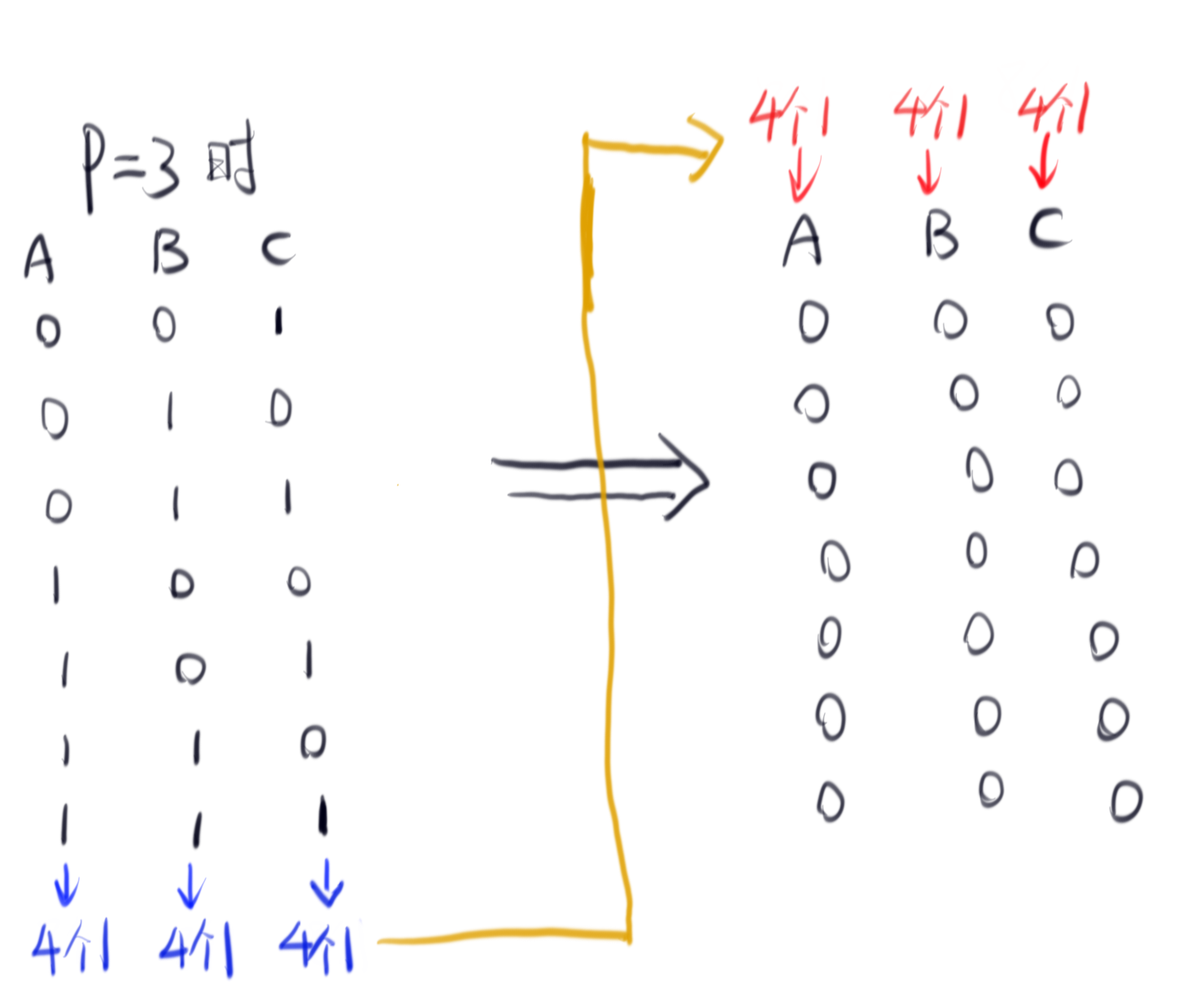
那么,这怎么填这个矩阵可以使整个乘积最小呢,当然相乘的数相互之间的差距越大越好,也就是我们要尽量保证多出现1(因为不能出现0,那1就是最小的数了):
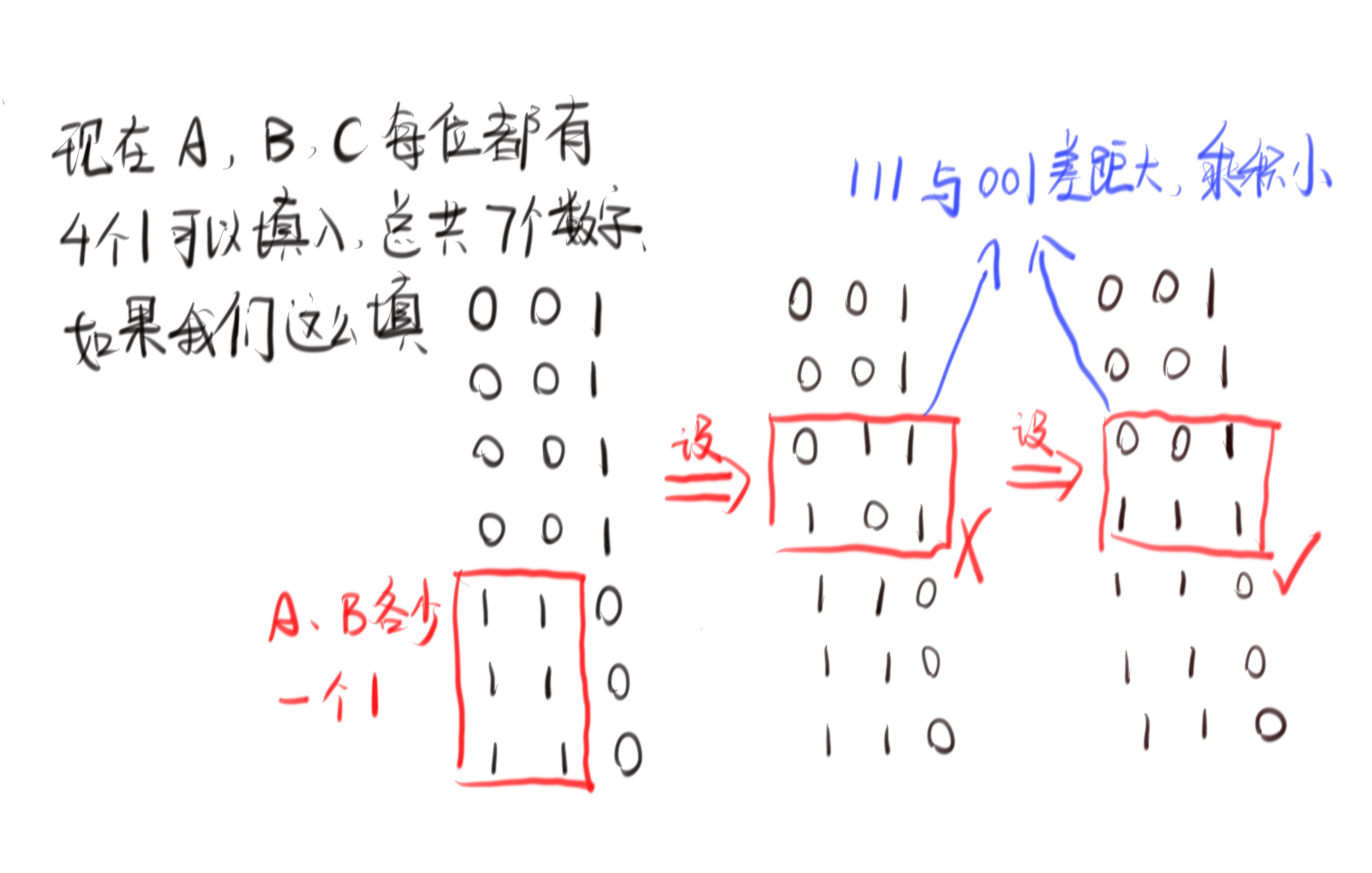
最后按照这个填法模拟一下p=4的情况:
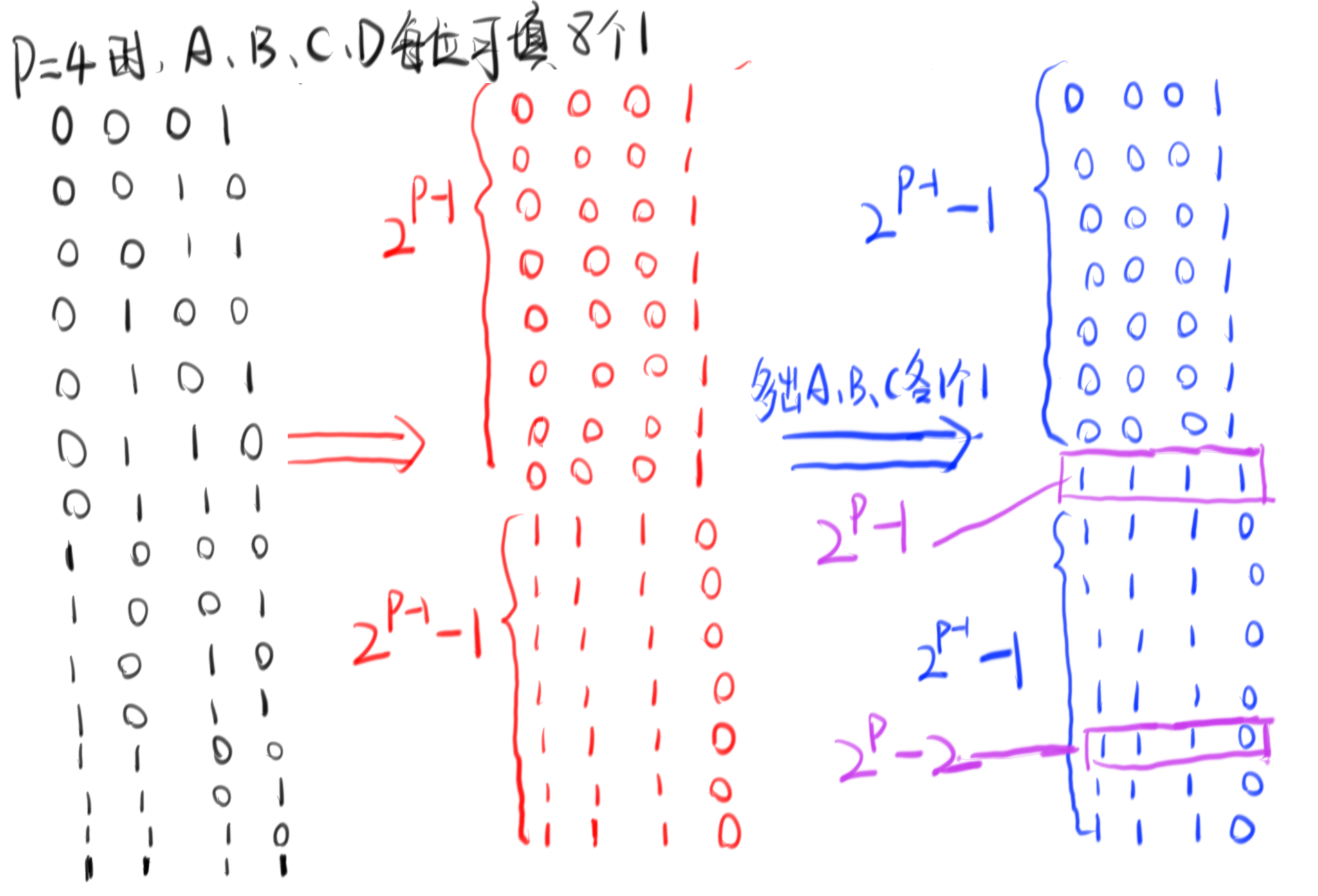
最后总结公式:
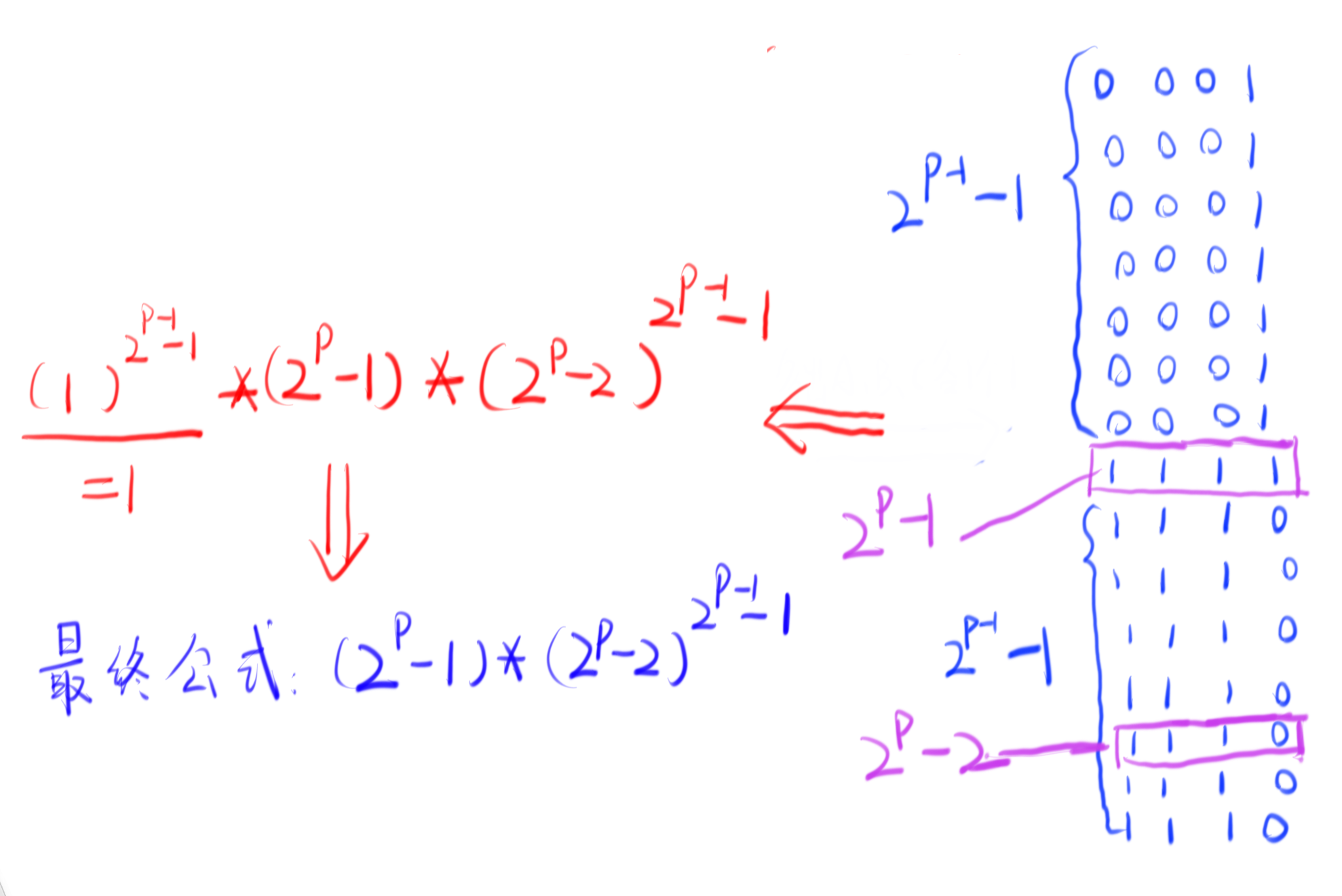
求幂次的操作可以使用快速幂完成,不过注意过程中会爆long long所以记得算一次取模一次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
typedef long long ll;
ll qmi(ll a,ll b){
ll ans=1,p=1e9+7;
while(b){
if(b&1) ans=(ans%p)*(a%p)%p;
b>>=1;
a=(a%p)*(a%p)%p;
}
return ans;
}
int minNonZeroProduct(int p) {
int mod=1e9+7;
return (((1ll<<p)-1)%mod)*(qmi((1ll<<p)-2,(1ll<<p-1)-1)%mod)%mod;
}
};
|
1970. 你能穿过矩阵的最后一天
题目
给你一个下标从 1 开始的二进制矩阵,其中 0 表示陆地,1 表示水域。同时给你 row 和 col 分别表示矩阵中行和列的数目。
一开始在第 0 天,整个 矩阵都是 陆地 。但每一天都会有一块新陆地被 水 淹没变成水域。给你一个下标从 1 开始的二维数组 cells ,其中 cells[i] = [ri, ci] 表示在第 i 天,第 ri 行 ci 列(下标都是从 1 开始)的陆地会变成 水域 (也就是 0 变成 1 )。
你想知道从矩阵最 上面 一行走到最 下面 一行,且只经过陆地格子的 最后一天 是哪一天。你可以从最上面一行的 任意 格子出发,到达最下面一行的 任意 格子。你只能沿着 四个 基本方向移动(也就是上下左右)。
请返回只经过陆地格子能从最 上面 一行走到最 下面 一行的 最后一天 。
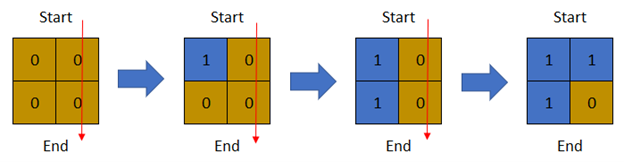
示例 1:
1
2
3
4
| 输入:row = 2, col = 2, cells =
输出:2
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 2 天。
|
示例 2:
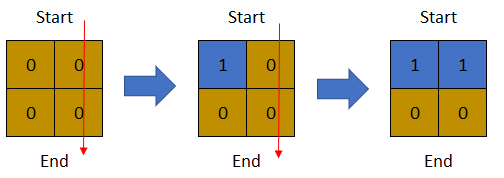
1
2
3
4
| 输入:row = 2, col = 2, cells =
输出:1
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 1 天。
|
示例 3:
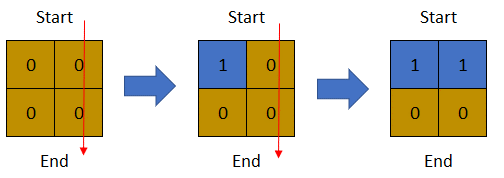
1
2
3
4
| 输入:row = 3, col = 3, cells =
输出:3
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 3 天。
|
提示:
2 <= row, col <= 2 10^4
4 <= row col <= 2 10^4
cells.length == row col
1 <= ri <= row
1 <= ci <= col
cells 中的所有格子坐标都是 唯一 的。
题解
这道题花了我很长时间,主要还是对时间复杂度估计不足。
首先我使用了BFS的方法,但是并没有使用去每张图上跑一遍BFS这么包里直接,而是做了一些改进:先从最后一张图中开始跑BFS,如果跑不到终点且BFS访问队列无法更新(说明路被海洋封死),那么我将队列中无法更新的点都记录下来,然后从最后一天往前倒退一天(将那一天的海洋变回陆地),再让那么点继续跑BFS,还是跑不到终点就继续往前倒回,一直反复到最终接近终点为止。
只可惜这个方法还是超时了……算是一种不那么好的思路吧,也在这放出来给大家对比对比(毕竟我写了N久不放太可惜了)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| class Solution {
public:
typedef pair<int,int> P;
int latestDayToCross(int n, int m, vector<vector<int>>& v) {
vector<vector<int>> g(n+10,vector<int>(m+10,0));
vector<vector<int>> vis(n+10,vector<int>(m+10,0));
for(auto& it:v) g[it[0]][it[1]]=1;
int dx[]={0,0,-1,1},dy[]={-1,1,0,0};
queue<P> que,back;
bool st=false;
for(int i=1;i<=m;i++)
if(g[1][i]==0)
st=true,que.push({1,i});
int ans=v.size();
while(!st){
ans--;
g[v[ans][0]][v[ans][1]]=0;
if(v[ans][0]==1){
que.push({v[ans][0],v[ans][1]});
st=true;
}
}
while(!que.empty()){
int x=que.front().first,y=que.front().second;
bool is_update=false;
if(x==n) break;
for(int i=0;i<4;i++){
int nx=x+dx[i],ny=y+dy[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!g[nx][ny]&&!vis[nx][ny]){
que.push({nx,ny});
vis[nx][ny]=1;
is_update=true;
}
}
if(!is_update) {back.push(que.front());que.pop();}
if(que.empty()){
ans--;
que=back;
while(!back.empty()) back.pop();
g[v[ans][0]][v[ans][1]]=0;
if(v[ans][0]==1) que.push({v[ans][0],v[ans][1]});
}
}
return ans;
}
};
|
超时之后我基本想不到什么优化的点子(毕竟在队列中点的保留那块已经优化到极致了),所以基本确定这个思路本身就有问题(因为这种非常规的BFS在下水平有限实在估不出具体的复杂度,只能说尝试了不行所以需要换条路)。
重新考虑后脑袋一拍想到了并查集,除了在构造方面复杂一些,并查集处理这个问题简直完美,只要对每条边的两端进行一个merge操作,就可以知道任意两个点之间是否连通(只要在一个集合内就必然是连通的)。对于天数上仍然使用从最后一天往回倒,先在最后一天的图上构建一个并查集(遍历整张图,对每条边的两端做merge操作),然后判断第一行的节点是否与最后一行的节点连通,不连通就往回倒一天,将那天海洋变回陆地并向周围merge一遍,反复如此即可。
需要注意,merge的时候要让编号大的节点做编号小的节点的父节点,这样find的时候只需要判断是不是最后一行就行了(因为一个集合的始祖节点一定是行数最高的节点)。
p2n函数是将行列转换为节点编号的函数,因为需要将二维数组的坐标转换为并查集的一维坐标。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Solution {
public:
typedef pair<int,int> P;
int n,m;
vector<int> f;
int p2n(int x,int y){
return x*m+y;
}
int find(int x){
return f[x]=x==f[x]?x:find(f[x]);
}
void merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy) return;
if(fx>fy) f[fy]=fx;
else f[fx]=fy;
}
int latestDayToCross(int row, int col, vector<vector<int>>& v) {
n=row,m=col;
vector<vector<int>> g(n+10,vector<int>(m+10,0));
for(auto& it:v) g[it[0]][it[1]]=1;
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
f=vector<int>((n+1)*(m+1),0);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
f[p2n(i,j)]=p2n(i,j);
int ans=v.size();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(g[i][j]==0)
for(int k=0;k<2;k++){
int nx=i+dx[k],ny=j+dy[k];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&g[nx][ny]==0)
merge(p2n(i,j),p2n(nx,ny));
}
bool st=true;
while(st){
for(int i=1;i<=m;i++)
if(find(p2n(1,i))>=p2n(n,m)-m+1){
st=false;
break;
}
if(!st) break;
ans--;
int x=v[ans][0],y=v[ans][1];
g[x][y]=0;
for(int i=0;i<4;i++){
int nx=x+dx[i],ny=y+dy[i];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&g[nx][ny]==0)
merge(p2n(x,y),p2n(nx,ny));
}
}
return ans;
}
};
|