Leetcode周赛第253场题解

周赛传送门

https://leetcode-cn.com/contest/weekly-contest-253/

俗话说：好汉不复当年勇，upper_bound玩不懂……咳咳咳。停了一年半的算法竞赛训练，明显感觉到自己的思路和代码能力退化了很多（果然考研会下降编程能力2333）。今天是复出（bushi）的第一（二）把Leetcode周赛，上周的周赛由于实在是太拉被我从记忆中删除了。话说现在力扣的神速哥真是越来越多了，他们AK的速度我怕是题目都读不完……

总结来讲今天的前两题都比较签到，第三题有一定的思考量，第四题是比较模板的一道题（虽然我菜到玩不明白upper_bound）。废话少说，进入题解！

5838. 检查字符串是否为数组前缀

题目

给你一个字符串 s 和一个字符串数组 words ，请你判断 s 是否为 words 的 前缀字符串 。

字符串 s 要成为 words 的 前缀字符串 ，需要满足：s 可以由 words 中的前 k（k 为 正数 ）个字符串按顺序相连得到，且 k 不超过 words.length 。

如果 s 是 words 的 前缀字符串 ，返回 true ；否则，返回 false 。

示例 1：

输入：s = "iloveleetcode", words = ["i","love","leetcode","apples"]
输出：true
解释：
s 可以由 "i"、"love" 和 "leetcode" 相连得到。

示例 2：

输入：s = "iloveleetcode", words = ["apples","i","love","leetcode"]
输出：false
解释：
数组的前缀相连无法得到 s 。

提示：

1 <= words.length <= 100
1 <= words[i].length <= 20
1 <= s.length <= 1000
words[i] 和 s 仅由小写英文字母组成

题解

这道题非常签到了，在字符串s数组上设置一个指针i，然后用words里每个word去匹配（用substr就很省事）。如果在遍历words过程中i能走到s的末尾就说明匹配上了，返回true；如果结束遍历了i还在字符串中间的位置，那么就匹配不上返回false。

class Solution {
public:
    bool isPrefixString(string s, vector<string>& words) {
        int i=0;
        for(auto& word:words){
            if(s.substr(i,word.length())==word) i+=word.length();
            else return false;
            if(i>=s.length()) return true;
        }
        return false;
    }
};

5839. 移除石子使总数最小

题目

给你一个整数数组 piles ，数组 下标从 0 开始 ，其中 piles[i] 表示第 i 堆石子中的石子数量。另给你一个整数 k ，请你执行下述操作 恰好 k 次：

选出任一石子堆 piles[i] ，并从中 移除 floor(piles[i] / 2) 颗石子。
注意：你可以对 同一堆 石子多次执行此操作。

返回执行 k 次操作后，剩下石子的 最小 总数。

floor(x) 为 小于 或 等于 x 的 最大 整数。（即，对 x 向下取整）。

示例 1：

输入：piles = [5,4,9], k = 2
输出：12
解释：可能的执行情景如下：

- 对第 2 堆石子执行移除操作，石子分布情况变成 [5,4,5] 。
- 对第 0 堆石子执行移除操作，石子分布情况变成 [3,4,5] 。
  剩下石子的总数为 12 。

示例 2：

输入：piles = [4,3,6,7], k = 3
输出：12
解释：可能的执行情景如下：

- 对第 2 堆石子执行移除操作，石子分布情况变成 [4,3,3,7] 。
- 对第 3 堆石子执行移除操作，石子分布情况变成 [4,3,3,4] 。
- 对第 0 堆石子执行移除操作，石子分布情况变成 [2,3,3,4] 。
  剩下石子的总数为 12 。

提示：

1 <= piles.length <= 10^5
1 <= piles[i] <= 10^4
1 <= k <= 10^5

题解

贪心即可，要想剩下的石子最少，那么就是拿走的石子最多。怎么拿走的石子最多呢，必然是每次拿最大堆的石头了，所以直接优先队列保证每次能拿最大就可以。

class Solution {
public:
    priority_queue<int> que;
    int minStoneSum(vector<int>& p, int k) {
        for(auto& x:p) que.push(x);
        while(k--){
            int x=que.top();que.pop();
            que.push(x-floor((float)x/2));
        }
        int sum=0;
        while(!que.empty()){
            sum+=que.top();
            que.pop();
        }
        return sum;
    }
};

5840. 使字符串平衡的最小交换次数

题目

给你一个字符串 s ，下标从 0 开始 ，且长度为偶数 n 。字符串 恰好 由 n / 2 个开括号 ‘[‘ 和 n / 2 个闭括号 ‘]’ 组成。

只有能满足下述所有条件的字符串才能称为 平衡字符串 ：

字符串是一个空字符串，或者
字符串可以记作 AB ，其中 A 和 B 都是 平衡字符串 ，或者
字符串可以写成 [C] ，其中 C 是一个 平衡字符串 。
你可以交换 任意 两个下标所对应的括号 任意 次数。

返回使 s 变成 平衡字符串 所需要的 最小 交换次数。

示例 1：

输入：s = "][]["
输出：1
解释：交换下标 0 和下标 3 对应的括号，可以使字符串变成平衡字符串。
最终字符串变成 "[[]]" 。

示例 2：

输入：s = "]]][[["
输出：2
解释：执行下述操作可以使字符串变成平衡字符串：
- 交换下标 0 和下标 4 对应的括号，s = "[]][[]" 。
- 交换下标 1 和下标 5 对应的括号，s = "[[][]]" 。
最终字符串变成 "[[][]]" 。

示例 3：

输入：s = "[]"
输出：0
解释：这个字符串已经是平衡字符串。

提示：

n == s.length
2 <= n <= 10^6
n 为偶数
s[i] 为’[‘ 或 ‘]’
开括号 ‘[‘ 的数目为 n / 2 ，闭括号 ‘]’ 的数目也是 n / 2

题解

首先这道题非常不错，我回忆起了古早时期我学过的关于匹配问题的一些知识。

对于括号匹配这种类似的问题，如果想成为合法的匹配序列，需要满足两个条件，在这之前我们先将[转换为数字-1，将]转换为数字1，这样我们就可以将括号转化为数组。

那么为什么要转化成数组的？因为这样就可以方便求前缀和数组了，并且前缀和数组才是最终目的，因为我们可以很轻易地从前缀和数组中发现序列是否合法匹配了。

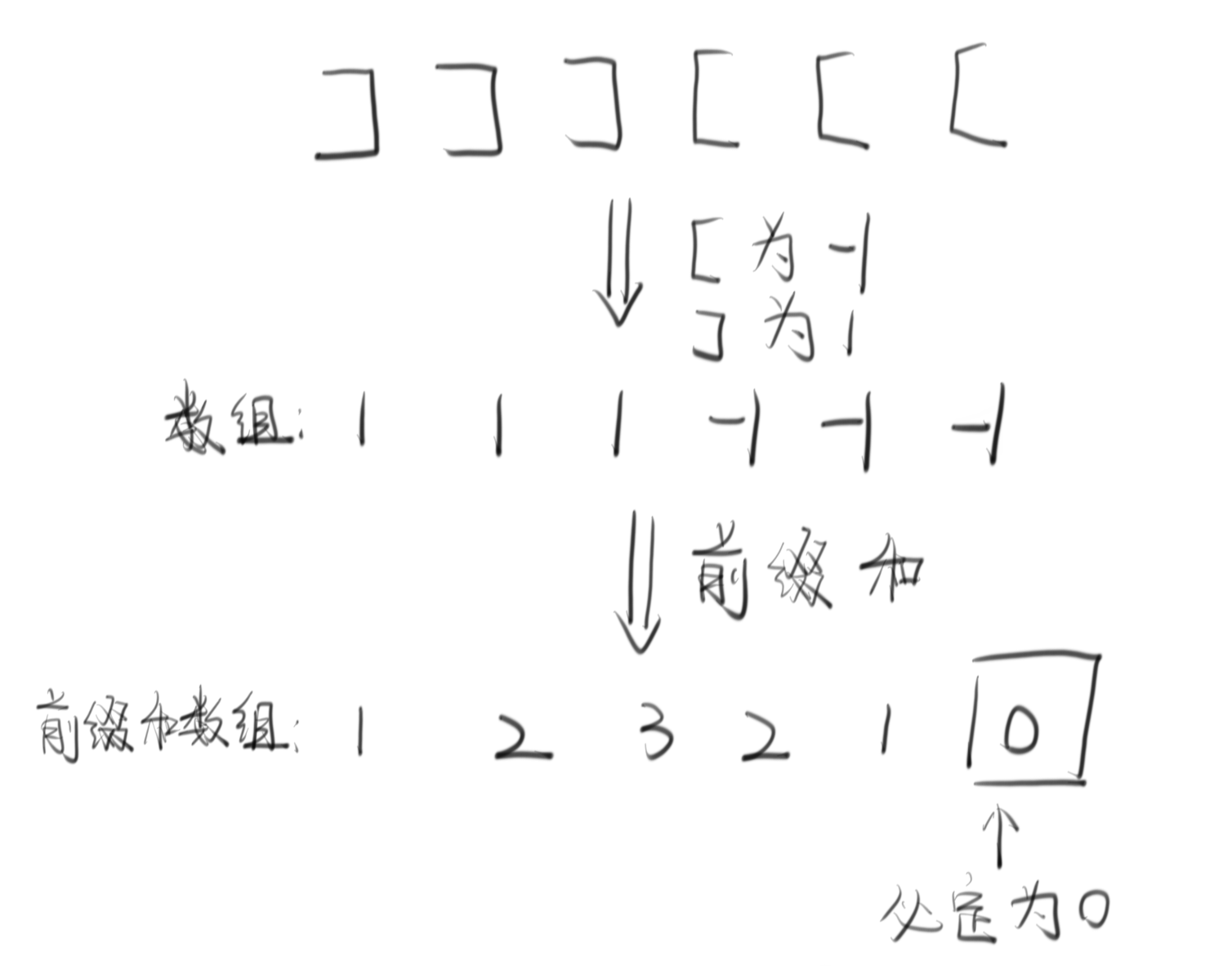
前缀和数组几乎是处理这种匹配问题的神器，因为可以立刻看出每个位置的匹配情况：

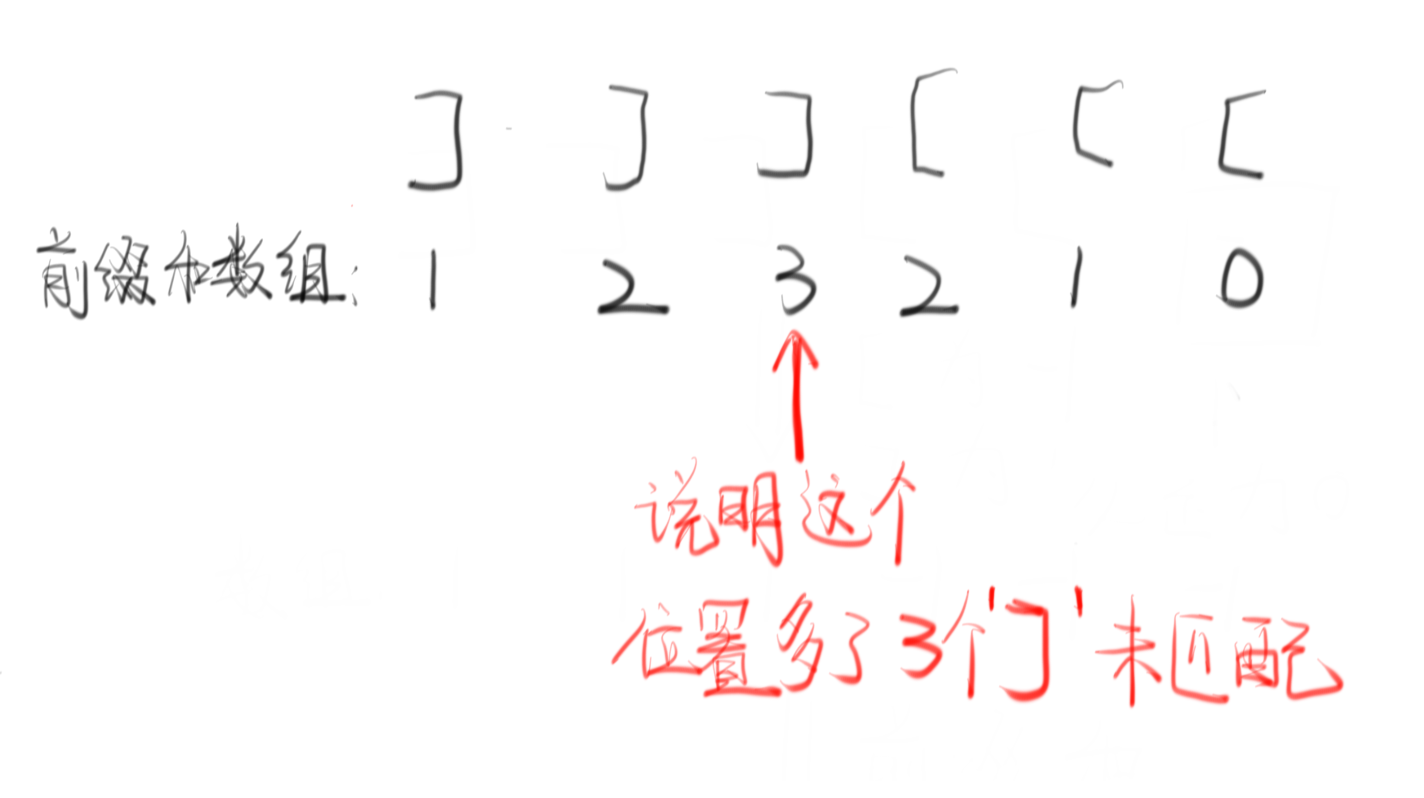
重要概念：对于一个正确匹配的括号序列的前缀和数组，应该满足两个条件：

• 不能出现大于0的元素（因为大于0说明当前位置有个右括号没匹配）
• 最后一个元素的值必须是0（说明序列没有多出没被右括号匹配的左括号）

这道题的话我们可以确保最后一个元素一定是0，因为题目说了字符串 恰好 由 n / 2 个开括号 ‘[‘ 和 n / 2 个闭括号 ‘]’ 组成。那我们只需要考虑怎么通过交换位置满足第一个条件即可。

那么就将交换放到前缀和数组场景下进行思考：

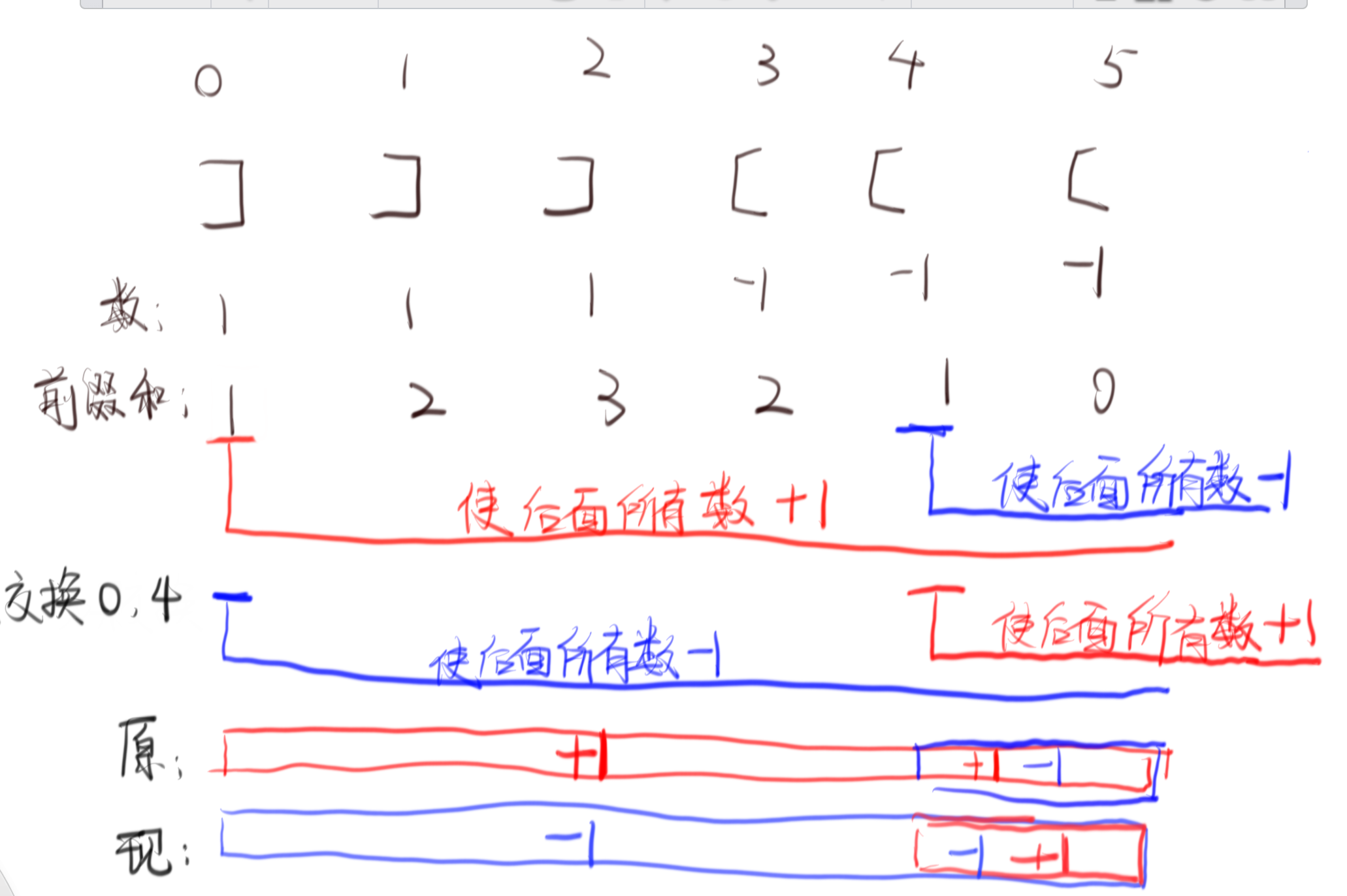
注意看红蓝大法！

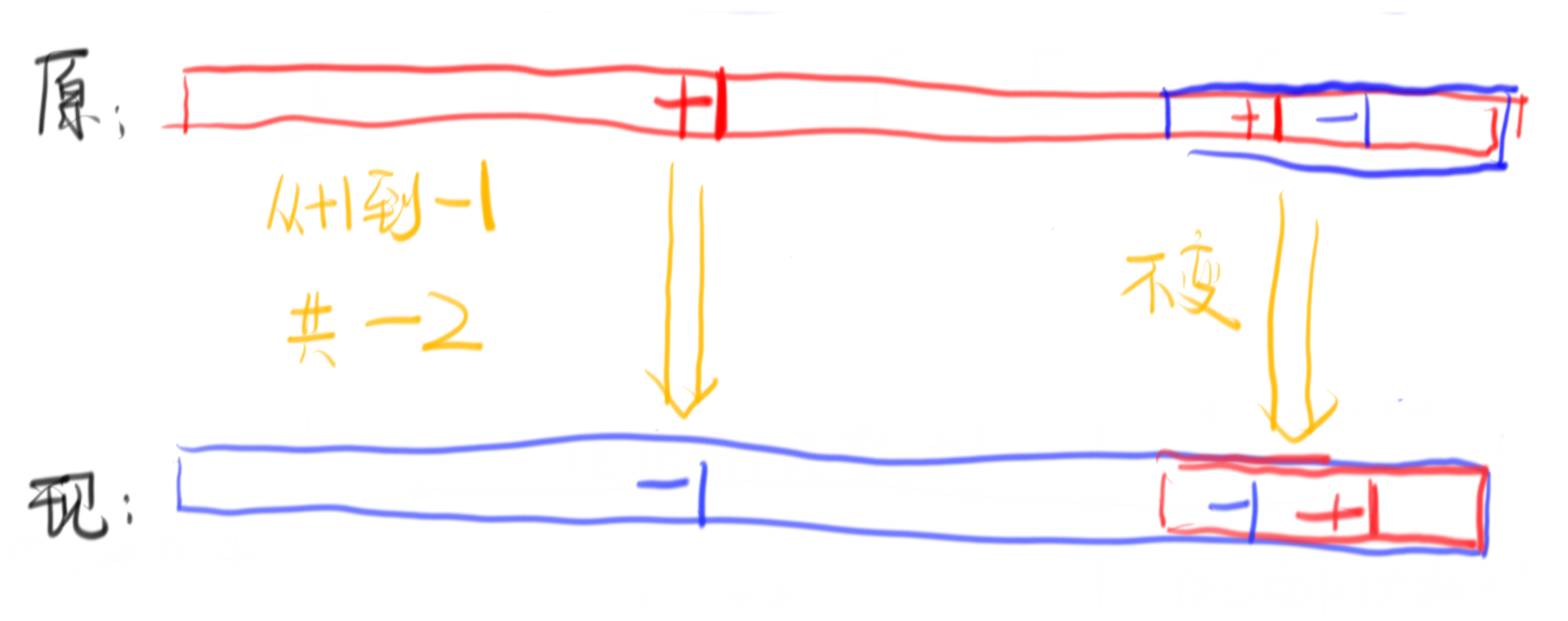
所以可以总结出如果交换a,b的位置，那么就是对前缀和数组[a,b)的元素进行-2操作，那么再结合前缀和中不能出现大于0的元素，我们就可以得出一个非常简单的结论：只需要找到前缀和数组中最大的那个数，看它能被几次-2操作减到小于等于0，这个次数就是答案了！再简单点，就是找到那个最大的元素除2向上取整！

当然，如果前缀和中没有大于0的元素，直接返回0，不需要换，已经符合条件了。

思维过程比较巧妙，代码非常简单：

class Solution {
public:
    int minSwaps(string s) {
        vector<int> v;
        for(auto& c:s){
            if(c=='[') v.push_back(-1);
            else v.push_back(1);
        }
        for(int i=1;i<v.size();i++) v[i]+=v[i-1];
        int mx=-1;
        for(auto& x:v) mx=max(mx,x);
        if(mx<=0) return 0;
        else{
            mx=ceil((float)mx/2.0);
            return mx;
        }
    }
};

5841. 找出到每个位置为止最长的有效障碍赛跑路线

题目

你打算构建一些障碍赛跑路线。给你一个 下标从 0 开始 的整数数组 obstacles ，数组长度为 n ，其中 obstacles[i] 表示第 i 个障碍的高度。

对于每个介于 0 和 n - 1 之间（包含 0 和 n - 1）的下标 i ，在满足下述条件的前提下，请你找出 obstacles 能构成的最长障碍路线的长度：

你可以选择下标介于 0 到 i 之间（包含 0 和 i）的任意个障碍。
在这条路线中，必须包含第 i 个障碍。
你必须按障碍在 obstacles 中的 出现顺序 布置这些障碍。
除第一个障碍外，路线中每个障碍的高度都必须和前一个障碍 相同 或者 更高 。
返回长度为 n 的答案数组 ans ，其中 ans[i] 是上面所述的下标 i 对应的最长障碍赛跑路线的长度。

示例 1：

输入：obstacles = [1,2,3,2]
输出：[1,2,3,3]
解释：每个位置的最长有效障碍路线是：

- i = 0: [1], [1] 长度为 1
- i = 1: [1,2], [1,2] 长度为 2
- i = 2: [1,2,3], [1,2,3] 长度为 3
- i = 3: [1,2,3,2], [1,2,2] 长度为 3

示例 2：

输入：obstacles = [2,2,1]
输出：[1,2,1]
解释：每个位置的最长有效障碍路线是：

- i = 0: [2], [2] 长度为 1
- i = 1: [2,2], [2,2] 长度为 2
- i = 2: [2,2,1], [1] 长度为 1

示例 3：

输入：obstacles = [3,1,5,6,4,2]
输出：[1,1,2,3,2,2]
解释：每个位置的最长有效障碍路线是：

- i = 0: [3], [3] 长度为 1
- i = 1: [3,1], [1] 长度为 1
- i = 2: [3,1,5], [3,5] 长度为 2, [1,5] 也是有效的障碍赛跑路线
- i = 3: [3,1,5,6], [3,5,6] 长度为 3, [1,5,6] 也是有效的障碍赛跑路线
- i = 4: [3,1,5,6,4], [3,4] 长度为 2, [1,4] 也是有效的障碍赛跑路线
- i = 5: [3,1,5,6,4,2], [1,2] 长度为 2

提示：

n == obstacles.length
1 <= n <= 10^5
1 <= obstacles[i] <= 10^7

题解

首先这是一道模板题，考察点就是最长上升子序列，一开始写了纯动态规划的算法超时了，先贴一下这个超时的$O(n^2)$的算法：

class Solution {
public:
    vector<int> longestObstacleCourseAtEachPosition(vector<int>& a) {
        vector<int> dp(a.size(),0);
        for(int i=0;i<a.size();i++){
            dp[i]=1;
            for(int j=0;j<i;j++)
                if(a[j]<=a[i])
                    dp[i]=max(dp[i],dp[j]+1);
        }  
        return dp;
    }
};

当然这个其实比较暴力的，所以超时了……

那么其实这道题是得优化到$O(nlogn)$的复杂度的，考虑下面的问题

然后进一步抽象这个问题：

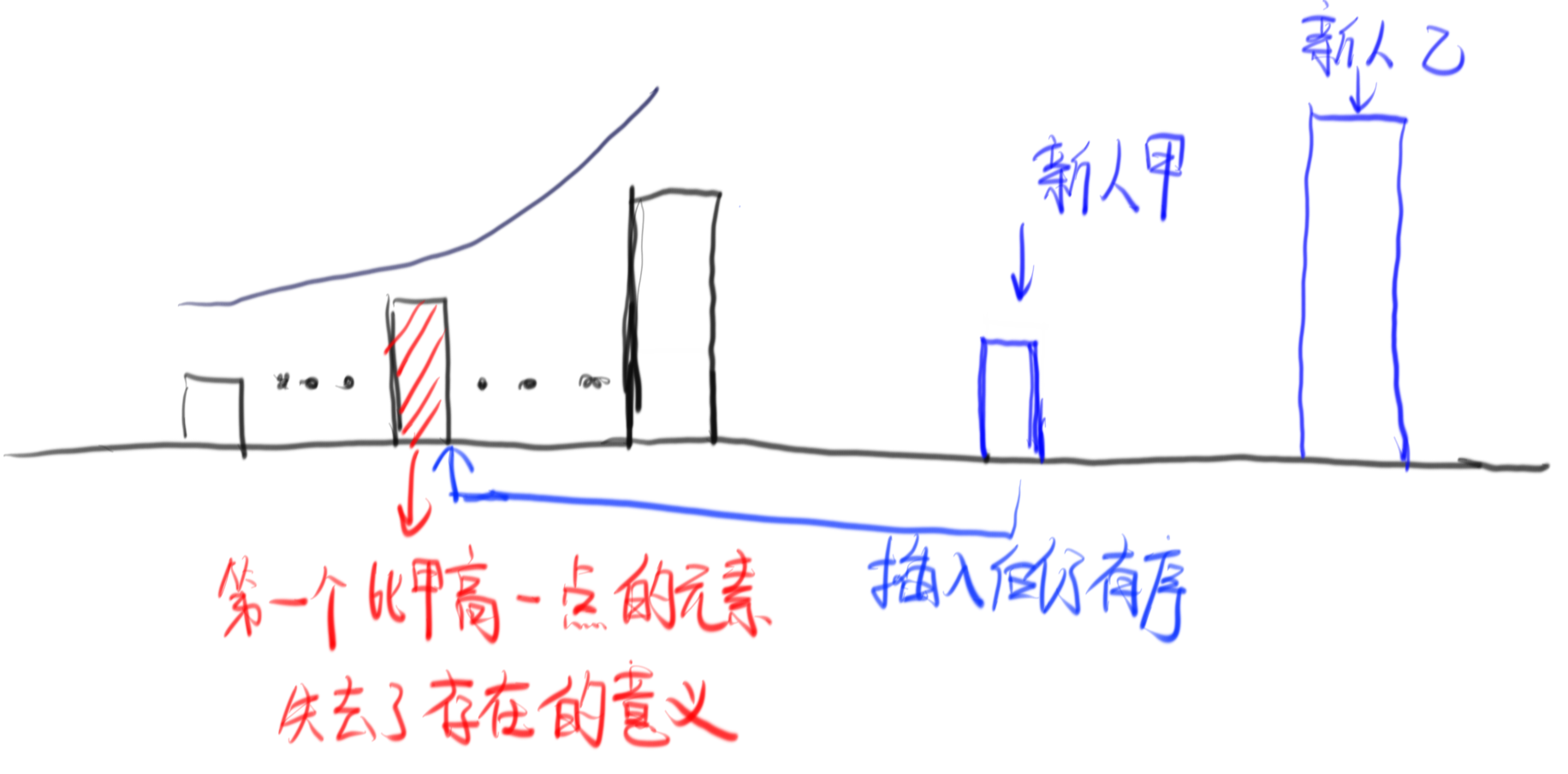
我们维护一个单调不减的序列作为，当有新元素加入时就将第一个比它的元素取而代之，可以简单拿一个例子证明一下为什么：

那么这样就可以证明新元素加入时第一个比它大的元素就可以下岗了。

这样，通过维护一个单调不减序列，就可以找到每个位置的单调不减序列长度了。

class Solution {
public:
    vector<int> longestObstacleCourseAtEachPosition(vector<int>& a) {
        vector<int> dp(a.size(),0);
        vector<int> v;
        for(int i=0;i<a.size();i++){
            if(v.size()==0||v.back()<=a[i]) v.push_back(a[i]),dp[i]=v.size();
            else{
                auto it=upper_bound(v.begin(),v.end(),a[i]);
                dp[i]=(int)(it-v.begin()+1);
                v[dp[i]-1]=a[i];
            }
        }  
        return dp;
    }
};