这次第三题有点划了,一开始还没看清题意纠结了十几分钟,然后又吃了一发TLE(超时),结束前才AC,马上下滑到了160名,狠啊
最后一题居然如此暴力,实在是在下所料未及,甘拜下风
周赛传送门
https://leetcode-cn.com/contest/weekly-contest-160
5238. 找出给定方程的正整数解
题目
给出一个函数 f(x, y) 和一个目标结果 z,请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。
给定函数是严格单调的,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)
函数接口定义如下:
1 | interface CustomFunction { |
如果你想自定义测试,你可以输入整数 function_id 和一个目标结果 z 作为输入,其中 function_id 表示一个隐藏函数列表中的一个函数编号,题目只会告诉你列表中的 2 个函数。
你可以将满足条件的 结果数对 按任意顺序返回。
题解
这题怕是一个阅读理解题,还好我做过leetcode类似的交互式题目,所以大概知道是什么意思,鉴于复杂度并不高,所以直接枚举x,y。如果f(x,y)==z就把答案加一
简单题不多说
1 | /* |
5239. 循环码排列
题目
给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,,...,2^n-1) 的排列 p,并且满足:
p[0] = startp[i]和p[i+1]的二进制表示形式只有一位不同p[0]和p[2^n -1]的二进制表示形式也只有一位不同
示例 1:
1 | 输入:n = 2, start = 3 |
示例 2:
1 | 输出:n = 3, start = 2 |
提示:
1 <= n <= 160 <= start < 2^n
题解
其实这题我觉得讲道理比第三题要难一些(好像事实证明确实第三题做出来的人要多一些?)
这一题考察的知识是《计算机组成原理》中的格雷码,大家可以自行百度一下格雷码的来历与定义,最关键的代码就是格雷码的生成,下面的代码就是生成n位格雷码的代码
1 | vector<int> create(int n){ |
如果想求出i的格雷码,只需要i^(i>>1)即可
接下来我们生成了n位数的所有格雷码,只需要找到起点,然后从起点开始转一圈就是答案了
下面是AC代码
1 | class Solution { |
5240. 串联字符串的最大长度
题目
给定一个字符串数组 arr,字符串 s 是将 arr 某一子序列字符串连接所得的字符串,如果 s 中的每一个字符都只出现过一次,那么它就是一个可行解。
请返回所有可行解 s 中最长长度。
示例 1:
1 | 输入:arr = ["un","iq","ue"] |
示例 2:
1 | 输入:arr = ["cha","r","act","ers"] |
示例 3:
1 | 输入:arr = ["abcdefghijklmnopqrstuvwxyz"] |
提示:
1 <= arr.length <= 161 <= arr[i].length <= 26arr[i]中只含有小写英文字母
题解
这题还是很暴力的,但是我一开始把题读错了QAQ
然后又吃了一发超时,亏大了
超时主要是因为我一开始使用二进制位运算来直接暴力组合,但是由于复杂度实在是太高,原以为能给我卡过去,但是Leetcode还是把它卡在了门外,然后我就去写n^2复杂度的枚举了
开一个set枚举即可,如果没有这些字符就把这个字符串的长度加到答案中去,有的话就不要加
可以提前扫一遍所有字符串把自己跟自己有重复的直接筛选掉
下面放上我情急之中的丑陋的代码
1 | class Solution { |
5241. 铺瓷砖
题目
你是一位施工队的工长,根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
房子的客厅大小为 n x m,为保持极简的风格,需要使用尽可能少的 正方形 瓷砖来铺盖地面。
假设正方形瓷砖的规格不限,边长都是整数。
请你帮设计师计算一下,最少需要用到多少块方形瓷砖?
示例 1:
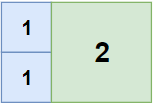
1 | 输入:n = 2, m = 3 |
示例 2:
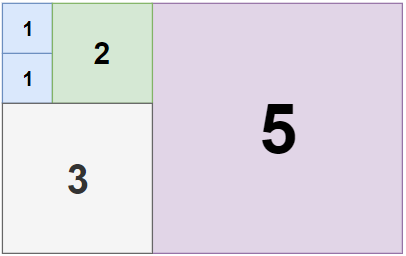
1 | 输入:n = 5, m = 8 |
示例 3:
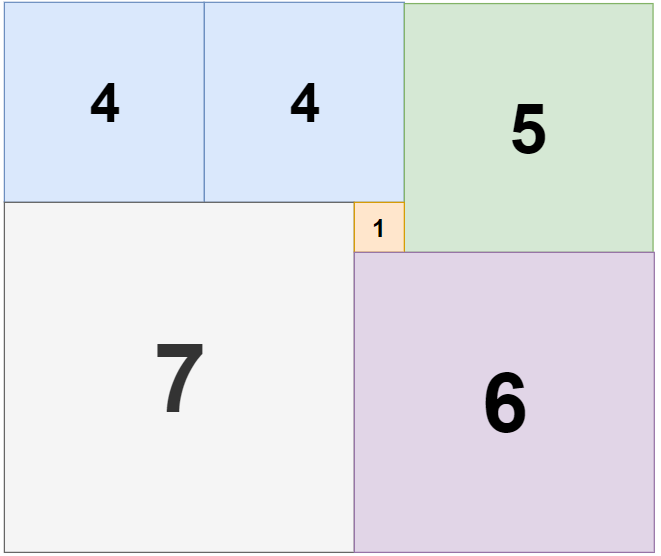
1 | 输入:n = 11, m = 13 |
提示:
1 <= n <= 131 <= m <= 13
题解
这一题可有意思了
这一题,让我们知道了什么叫人有多大胆,地有多大产
这一题,让我们知道了搏一搏,单车变摩托
这一题,让我们知道了暴力出奇迹
我现在诚挚推出最后一题的算法
打!!表!!
没错,你没有听错,13x13这么小的复杂度,打就完了
疯狂枚举,枚举,枚举
首先我们枚举横向的分割线
然后再枚举纵向的分割线
最后再超级加倍枚举中间的正方形
就是下面的图(来自于热心网友的题解)
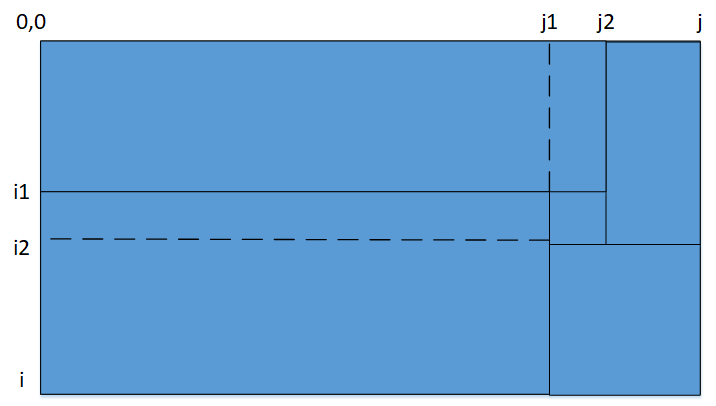
当然我们是一个有节操的人,我们还是需要记忆化搜索一下降低复杂度的
最后上打表的代码
1 |
|
下面是AC的代码,就是把打表代码的输出搬上去而已
1 | class Solution { |
下周见!See you!