In The End

个人博客

0%

ACM数据结构

发表于 更新于 分类于

单链表

链表和数组都可用于存储数据，其中链表通过指针来连接元素，而数组则是把所有元素按次序依次存储。

不同的存储结构令他们有了不同的优势：

链表可以方便地删除、插入数据，操作次数是$O(1)$。但也因为这样寻找读取数据的效率不如数组高，在随机访问数据中的操作次数是$O(n)$

数组可以方便的寻找读取数据，在随机访问中操作次数是$O(1)$。但删除、插入的操作次数却是却是$O(n)$​次

数组模拟单链表

例题

https://www.acwing.com/problem/content/828/

思路

众所周知链表可以用结构体+指针来实现

但是由于malloc和new单个节点很浪费时间，所以在竞赛中一般都使用数组模拟单链表

下面是模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数a
void insert(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

head存储头节点（初始为-1指向空），e数组存储数值，ne数组存储下一个位置（相当于next指针）

注意：idx存储的是节点的编号（从0开始），是按照节点的创建顺序排序的，这道题刚好可以用上，其他的应用一般不太用得上

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int e[maxn],ne[maxn],head,idx;

void init(){
    head=-1;
    idx=0;
}

void add_to_head(int x){
    e[idx]=x;
    ne[idx]=head;
    head=idx++;
}

void add(int k,int x){
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx++;
}

void remove(int k){
    ne[k]=ne[ne[k]];
}

int main(){
    int n,k,x;
    char c;
    init();
    cin>>n;
    while(n--){
        cin>>c;
        if(c=='H'){
            cin>>x;
            add_to_head(x);
        }
        else if(c=='I'){
            cin>>k>>x;
            add(k-1,x);
        }
        else{
            cin>>k;
            if(!k) head=ne[head];
            else remove(k-1);
        }
    }
    for(int i=head;i!=-1;i=ne[i]){
        if(i!=head) cout << ' ';
        cout << e[i];
    }
    cout << endl;
    return 0;
}

双链表

双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点

数组模拟双链表

例题

https://www.acwing.com/problem/content/829/

思路

我们延续上面的数组模拟单链表的思路，但是因为是双链表，所以我们需要设置两个空节点，我们将这两个节点的idx赋值为0和1，然后我们idx从2开始递增，这样就在左右添加了两个哨兵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

注意：因为这道题需要操作第k个插入的数，因为我们idx起始值为2了，所以所有对k的操作相当于对k+1操作

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int l[maxn],r[maxn],e[maxn],idx;

void init(){
    r[0]=1;
    l[1]=0;
    idx=2;
}

void insertR(int k,int x){
    e[idx]=x;
    l[idx]=k,r[idx]=r[k];
    l[r[k]]=idx,r[k]=idx++;
}

void insertL(int k,int x){
    insertR(l[k],x);
}

void addL(int x){
    insertR(0,x);
}

void addR(int x){
    insertL(1,x);
}


void remove(int k){
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}

int main(){
    int n,k,x;
    string s;
    init();
    cin>>n;
    while(n--){
        cin>>s;
        if(s=="L"){
            cin>>x;
            addL(x);
        }
        else if(s=="R"){
            cin>>x;
            addR(x);
        }
        else if(s=="D"){
            cin>>k;
            remove(k+1);
        }
        else if(s=="IL"){
            cin>>k>>x;
            insertL(k+1,x);
        }
        else{
            cin>>k>>x;
            insertR(k+1,x);
        }
    }
    for(int i=r[0];i!=1;i=r[i]){
        if(i!=r[0]) cout << ' ';
        cout << e[i];
    }
    cout << endl;
    return 0;
}

栈

数组模拟栈

例题

https://www.acwing.com/problem/content/830/

思路

栈的修改是按照后进先出的原则进行的，因此栈通常被称为是后进先出（last in first out）表，简称 LIFO 表

数组模拟栈，这个就不多说了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0)
{

}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int s[maxn],t;

void push(int x){
    s[t++]=x;
}

int query(){
    return s[t-1];
}

void pop(){
    t--;
}

bool empty(){
    return t==0;
}

int main(){
    int n,x;
    string str;
    cin>>n;
    while(n--){
        cin>>str;
        if(str=="push"){
            cin>>x;
            push(x);
        }
        else if(str=="query")
            cout << query() << endl;
        else if(str=="pop")
            pop();
        else{
            if(empty())
                cout << "YES" << endl;
            else
                cout << "NO" << endl;
        }
    }
    return 0;
}

单调栈

例题

https://www.acwing.com/problem/content/832/

思路

单调栈即满足单调性的栈结构。与单调队列相比，其只在一端进行进出

一般单调栈的用途就是找到每个数左边或者右边第一个比它小(大)的数字

1
2
3
4
5
6
7
常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(q[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int s[maxn],t;

int main(){
    int n,x;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&x);
        while(t&&s[t-1]>=x) t--;
        if(t) printf("%d ",s[t-1]);
        else printf("-1 ");
        s[t++]=x;
    }
    printf("\n");
    return 0;
}

队列

数组模拟队列

例题

https://www.acwing.com/problem/content/831/

思路

先进入队列的元素一定先出队列，因此队列通常也被称为先进先出（first in first out）表，简称 FIFO 表

数组模拟队列，这个也不多说了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt)
{

}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int s[maxn],head,rear;

void push(int x){
    s[rear++]=x;
}

int query(){
    return s[head];
}

void pop(){
    head++;
}

bool empty(){
    return head==rear;
}

int main(){
    int n,x;
    string str;
    cin>>n;
    while(n--){
        cin>>str;
        if(str=="push"){
            cin>>x;
            push(x);
        }
        else if(str=="query")
            cout << query() << endl;
        else if(str=="pop")
            pop();
        else{
            if(empty())
                cout << "YES" << endl;
            else
                cout << "NO" << endl;
        }
    }
    return 0;
}

单调队列

例题

https://www.acwing.com/problem/content/156/

思路

“单调” 指的是元素的的 “规律”——递增（或递减）

“队列” 指的是元素只能从队头和队尾进行操作

要求的是每连续的$k$个数中的最大（最小）值，很明显，当一个数进入所要 “寻找” 最大值的范围中时，若这个数比其前面（先进队）的数要大，显然，前面的数会比这个数先出队且不再可能是最大值

也就是说——当满足以上条件时，可将前面的数 “弹出”，再将该数真正 push 进队尾

这就相当于维护了一个递减的队列，符合单调队列的定义，减少了重复的比较次数，不仅如此，由于维护出的队伍是查询范围内的且是递减的，队头必定是该查询区域内的最大值，因此输出时只需输出队头即可

显而易见的是，在这样的算法中，每个数只要进队与出队各一次，因此时间复杂度被降到了$O(n)$

而由于查询区间长度是固定的，超出查询空间的值再大也不能输出，因此还需要 site 数组记录第$i$个队中的数在原数组中的位置，以弹出越界的队头。

注意：这里的队列并不能用STL的queue实现，因为需要弹出队尾元素，所以我们可以用STL的deque实现，即双端队列

1
2
3
4
5
6
7
8
常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
using namespace std;
const int maxn=1e6+10;

int a[maxn],q[maxn],head,rear;

int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    for(int i=0;i<n;i++){
        if(rear>head&&i-k+1>q[head]) head++;
        while(rear>head&&a[q[rear-1]]>=a[i]) rear--;
        q[rear++]=i;
        if(i>=k-1) printf("%d ",a[q[head]]);
    }
    printf("\n");
    head=rear=0;
    for(int i=0;i<n;i++){
        if(rear>head&&i-k+1>q[head]) head++;
        while(rear>head&&a[q[rear-1]]<=a[i]) rear--;
        q[rear++]=i;
        if(i>=k-1) printf("%d ",a[q[head]]);
    }
    printf("\n");
    return 0;
}

KMP

KMP字符串

例题

https://www.acwing.com/problem/content/833/

思路

市面上其实有两种next数组的构造方法，一种是从-1开始，一种是从0开始

下面的模板是从-1开始的，我觉得更好理解一些

KMP的思维非常抽象和复杂，来日再补

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
求Next数组：
// s[]是模式串，p[]是模板串, n是s的长度，m是p的长度
void pre_kmp(){
    int i=0,j=-1;
    ne[0]=-1;
    while(i<n){
        while(j>-1&&p[i]!=p[j]) j=ne[j];
        ne[++i]=++j;
    }
}

// 匹配
void kmp(){
    int i=0,j=0;
    while(i<m){
        while(j>-1&&s[i]!=p[j]) j=ne[j];
        if(j==n-1){
            //匹配成功后的逻辑
            j=ne[j];
        }
        i++,j++;
    }
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
using namespace std;
const int M=1e5+10,N=1e4+10;

int n,m;
char p[N],s[M];
int ne[N];

void pre_kmp(){
    int i=0,j=-1;
    ne[0]=-1;
    while(i<n){
        while(j>-1&&p[i]!=p[j]) j=ne[j];
        ne[++i]=++j;
    }
}

void kmp(){
    int i=0,j=0;
    while(i<m){
        while(j>-1&&s[i]!=p[j]) j=ne[j];
        if(j==n-1){
            printf("%d ",i-n+1);
            j=ne[j];
        }
        i++,j++;
    }
    printf("\n");
}

int main(){
    scanf("%d%s%d%s",&n,p,&m,s);
    pre_kmp();
    kmp();
    return 0;
}

Trie(前缀树/字典树)

Trie字符串统计

例题

https://www.acwing.com/problem/content/837/

思路

img

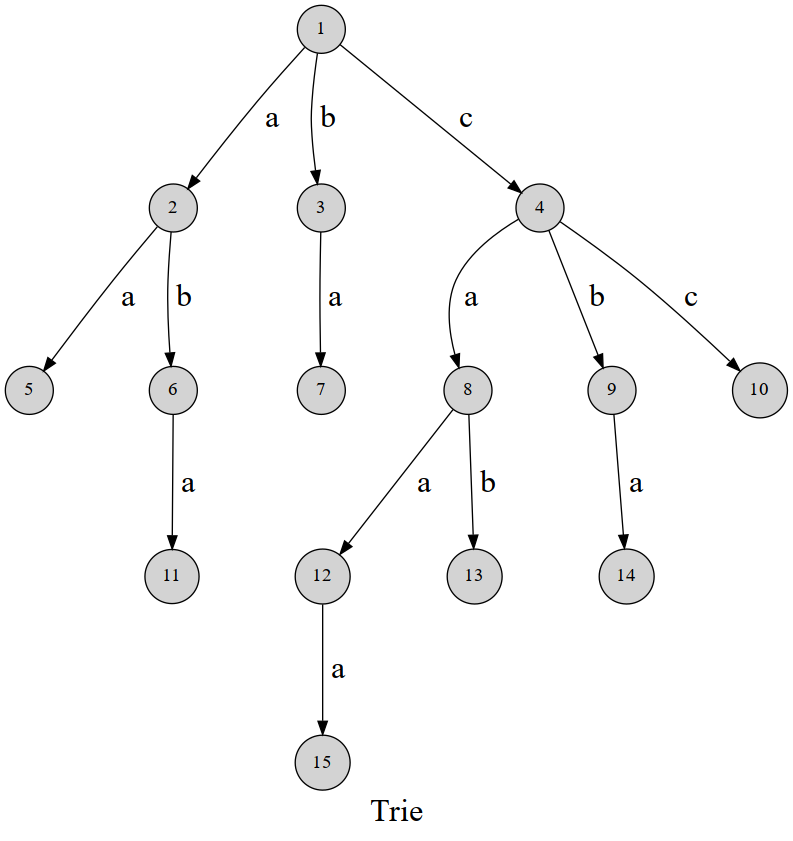
上面这张图就是字典树Trie的全貌了

可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子，$1\to4\to8\to12$表示的就是字符串 caa 。

Trie 的结构非常好懂，我们用一个二维数组$son[i,j]$表示结点 i 的 j 字符指向的下一个结点，或着说是结点 i 代表的字符串后面添加一个字符 j 形成的字符串的结点。（j 的取值和字符集大小有关，不一定是 $0\sim26$）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
using namespace std;
const int maxn=1e5+10;

int son[maxn][26],cnt[maxn],idx;
char str[maxn];

void insert(char *s){
    int p=0;
    for(int i=0;s[i];i++){
        int u=s[i]-'a';
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}

int query(char* s){
    int p=0;
    for(int i=0;s[i];i++){
        int u=s[i]-'a';
        if(!son[p][u]) return 0;
        p=son[p][u];
    }
    return cnt[p];
}

int main(){
    int n;
    char op[2];
    scanf("%d",&n);
    while(n--){
        scanf("%s%s",op,str);
        if(op[0]=='I')
            insert(str);
        else
            printf("%d\n",query(str));
    }
    return 0;
}

最大异或对

例题

https://www.acwing.com/problem/content/145/

思路

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;

int son[N*32][2],cnt[N*32],idx,a[N];

void insert(int a){
    int p=0;
    for(int i=31;i>=0;i--){
        int u=(a>>i)&1;
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}

int query(int a){
    int p=0,ans=0;
    for(int i=31;i>=0;i--){
        int u=(a>>i)&1;
        if(son[p][!u])
            p=son[p][!u],ans+=(1<<i);
        else
            p=son[p][u];
    }
    return ans;
}

int main(){
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
        insert(a[i]);
    }
    int ans=0;
    for(int i=0;i<n;i++)
        ans=max(ans,query(a[i]));
    printf("%d\n",ans);
    return 0;
}