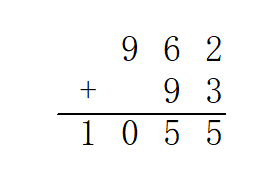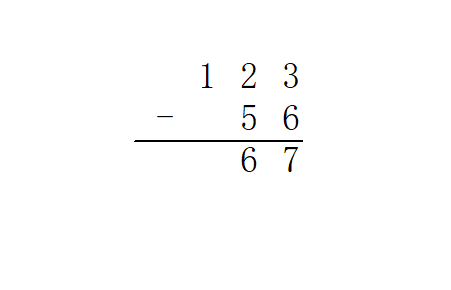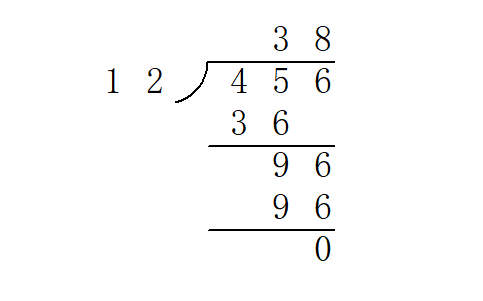快速排序

例题

https://www.acwing.com/problem/content/787/

思路

这里默认为升序排序，降序只要对比较的符号进行调整就可以了

快速排序分为三个过程：

将数列划分为两部分（不是直接分，要求保证相对大小关系）
递归到两个子序列中分别进行快速排序
不用合并，因为此时数列已经完全有序

首先对于第一步来说我们需要先找到一个基准值（基准值用于将整个数组切分成小和大两部分）

然后使用两个指针$i$和$j$来进行操作，大概原理就是先将$i$指向$l-1$的位置，$j$指向$r+1$的位置，然后使用do while循环使i指针疯狂向前直到遇到第一个比基准值大的数字停下，接下来对j指针也同样操作使其停在第一个比基准值小的数值上，然后互换$i$，$j$的数字。一直操作到ij指针相遇，那么由于对一路上不符合条件的数字都进行了互换，所以i和j相遇的就是整个数组的切分点。

OK我们找到了切分点，接下来就是递归操作$(l,j),(j+1,r)$了

注意事项：当切分点取$a[l]$时，递归取$(l,j),(j+1,r)$。当切分点取$a[r]$时，递归取$(l,i-1),(i,r)$。当切分点其余数字时，递归二者皆可(避免出现死循环)

每个递归直到l>=r停止，因为一个点是不需要再“划分”的

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn],n;

void quick_sort(int l,int r){
    if(l>=r) return;
    int x=a[l],i=l-1,j=r+1;
    while(i<j){
        do i++; while(a[i]<x);
        do j--; while(a[j]>x);
        if(i<j) swap(a[i],a[j]);
    }
    quick_sort(l,j);
    quick_sort(j+1,r);
}

int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    quick_sort(0,n-1);
    for(int i=0;i<n;i++) printf("%d ",a[i]);
    return 0;
}

线性第K大

例题

https://www.acwing.com/problem/content/788/

思路

找第 k 大的数（K-th order statistic），最简单的方法是先排序，然后直接找到第 k 大的位置的元素。这样做的时间复杂度是$O(nlogn)$，对于这个问题来说很不划算。事实上，我们有时间复杂度 $O(n)$的解法。

考虑快速排序的划分过程，在快速排序的“划分”结束后，我们会将数组分成两部分，我们可以通过检查k是否落在左边的范围内来减少复杂度，在排序的途中解决这个问题，当然这时候快排就不会全部排完了，而是找到了k就中途退出

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn];

int quick_sort(int l,int r,int k){
    if(l==r&&l==k) return a[k];
    int x=a[l],i=l-1,j=r+1;
    while(i<j){
        do i++; while(a[i]<x);
        do j--; while(a[j]>x);
        if(i<j) swap(a[i],a[j]);
    }
    if(l<=k&&k<=j) quick_sort(l,j,k);
    else quick_sort(j+1,r,k);
}

int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    printf("%d\n",quick_sort(0,n-1,k-1));
    return 0;
}

归并排序

例题

https://www.acwing.com/problem/content/789/

思路

归并排序是一种采用了分治思想的排序算法，其本质是一种 CDQ 分治。

归并排序分为三个过程：

将数列随意划分为两部分（在均匀划分时时间复杂度为 $O(nlogn)$ ）
递归地分别对两个子序列进行归并排序
合并两个子序列

不难发现，归并排序的核心是如何合并两个子序列，前两步都很好实现。

其实合并的时候也不难操作。注意到两个子序列在第二步中已经保证了都是有序的了，第三步中实际上是想要把两个有序的序列合并起来。

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn],t[maxn];

void merge_sort(int l,int r){
    if(l>=r) return;
    int mid=l+r>>1;
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r){
        if(a[i]<=a[j]) t[k++]=a[i++];
        else t[k++]=a[j++];
    }
    while(i<=mid) t[k++]=a[i++];
    while(j<=r) t[k++]=a[j++];
    for(int i=l,j=0;j<k;i++,j++)
        a[i]=t[j];
}

int main(){
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    merge_sort(0,n-1);
    for(int i=0;i<n;i++)
        printf("%d ",a[i]);
    printf("\n");
    return 0;
}

逆序对

例题

https://www.acwing.com/problem/content/790/

思路

归并排序还可以用来求逆序对的个数。

所谓逆序对，就是满足$a[i]>a[j]$且$i<j$的数对。

可以用 树状数组、线段树等数据结构来求，也可以用归并排序来求。

具体来说，下面归并排序ans+=mid-i+1就是在统计逆序对个数。

是因为，那里把靠后的数放到前面了（较小的数放在前面），所以在这个数的原来位置之前的、比它大的数都会和它形成逆序对，而这个个数就是还没有合并进去的数的个数，即为 mid - p 。

使用归并排序求逆序对的时间复杂度也是$O(nlogn)$。

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;
typedef long long ll;

int a[maxn],t[maxn];

ll merge_sort(int l,int r){
    if(l>=r) return 0;
    ll ans=0;
    int mid=l+r>>1;
    ans+=merge_sort(l,mid);
    ans+=merge_sort(mid+1,r);
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r){
        if(a[i]<=a[j]) t[k++]=a[i++];
        else t[k++]=a[j++],ans+=mid-i+1;
    }
    while(i<=mid) t[k++]=a[i++];
    while(j<=r) t[k++]=a[j++];
    for(int i=l,j=0;j<k;i++,j++) a[i]=t[j];
    return ans;
}

int main(){
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    ll ans=merge_sort(0,n-1);
    printf("%lld\n",ans);
    return 0;
}

二分

整数二分

例题

https://www.acwing.com/problem/content/791/

思路

二分搜索，也称折半搜索、二分查找，是用来在一个有序数组中查找某一元素的算法。

以在一个升序数组中查找一个数为例。

它每次考察数组当前部分的中间元素，如果中间元素刚好是要找的，就结束搜索过程；如果中间元素小于所查找的值，那么左侧的只会更小，不会有所查找的元素，只需要到右侧去找就好了；如果中间元素大于所查找的值，同理，右侧的只会更大而不会有所查找的元素，所以只需要到左侧去找。

在二分搜索过程中，每次都把查询的区间减半，因此对于一个长度为n的数组，至多会进行O(logn)次查找。

下面是第一种整数二分形式，用于找到>=x的区间的第一个数

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

下面是第二种整数二分形式，用于找到<=x的最后一个数

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn];

int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    while(m--){
        int x;
        scanf("%d",&x);
        int l=0,r=n-1;
        while(l<r){
            int mid=l+r>>1;
            if(a[mid]>=x) r=mid;
            else l=mid+1;
        }
        if(a[l]!=x) {puts("-1 -1");continue;}
        else printf("%d ",l);
        l=0,r=n-1;
        while(l<r){
            int mid=l+r+1>>1;
            if(a[mid]<=x) l=mid;
            else r=mid-1;
        }
        printf("%d\n",l);
    }
    return 0;
}

实数二分

例题

https://www.acwing.com/problem/content/792/

思路

实数二分比整数二分好写很多，因为不需要在乎细节(不用管加一减一的边界条件，因为是实数集)

所有的都是l=mid和r=mid，因为实数集不用考虑整数情况下的死循环问题

通常为了让实数集上的二分能够结束，我们有卡精度和卡迭代次数两种方法

注意：这道题需要对负数进行特殊处理，先当正数算出答案后把答案再变成负数

模板

卡精度

#include <iostream>
#include <cmath>
using namespace std;

int main(){
    double n;
    bool minus=false;
    scanf("%lf",&n);
    if(n<0) minus=true,n=-n;
    double l=0,r=n;
    while(r-l>1e-8){
        double mid=(l+r)/2;
        if(pow(mid,3)>=n) r=mid;
        else l=mid;
    }
    if(minus) l=-l;
    printf("%.6lf\n",l);
    return 0;
}

卡迭代次数

#include <iostream>
#include <cmath>
using namespace std;

int main(){
    double n;
    bool minus=false;
    scanf("%lf",&n);
    if(n<0) minus=true,n=-n;
    double l=0,r=n;
    for(int i=0;i<100;i++){
        double mid=(l+r)/2;
        if(pow(mid,3)>=n) r=mid;
        else l=mid;
    }
    if(minus) l=-l;
    printf("%.6lf\n",l);
    return 0;
}

高精度

我们使用vector\来存储高精度数字，vector的每一个数字表示一位

因为数字的长度可能发生变化，但我们希望同样权值位始终保持对齐（例如，希望所有的个位都在下标 [0] ，所有的十位都在下标 [1]……）；同时，加、减、乘的运算一般都从个位开始进行，这都给了「反转存储」以充分的理由。

所以我们的vector是从低位到高位存储的，反一下

高精度加法

例题

https://www.acwing.com/problem/content/793/

思路

高精度加法，其实就是竖式加法啦。

也就是从最低位开始，将两个加数对应位置上的数码相加，并判断是否达到或超过$10$。如果达到，那么处理进位：将更高一位的结果上增加$1$，当前位的结果减少$10$ 。

模板

#include <iostream>
#include <vector>
using namespace std;

vector<int> add(vector<int>& a,vector<int>& b){
    int t=0;
    vector<int> ans;
    for(int i=0;i<a.size()||i<b.size();i++){
        if(i<a.size()) t+=a[i];
        if(i<b.size()) t+=b[i];
        ans.push_back(t%10);
        t/=10;
    }
    if(t) ans.push_back(1);
    return ans;
}

int main(){
    string sa,sb;
    vector<int> a,b;
    cin>>sa>>sb;
    for(int i=sa.length()-1;i>=0;i--) a.push_back(sa[i]-'0');
    for(int i=sb.length()-1;i>=0;i--) b.push_back(sb[i]-'0');
    vector<int> ans=add(a,b);
    for(int i=ans.size()-1;i>=0;i--)
        cout << ans[i];
    cout << endl;
    return 0;
}

高精度减法

例题

https://www.acwing.com/problem/content/794/

思路

高精度减法，也就是竖式减法啦。

从个位起逐位相减，遇到负的情况则向上一位借。整体思路与加法完全一致。

注意：我们需要首先实现一个比较两个高精度数字大小的一个函数，因为有可能会出现相减为负数的情况，需要特殊考虑

模板

#include <iostream>
#include <vector>
using namespace std;

bool cmp(vector<int>& a,vector<int>& b){
    if(a.size()!=b.size()) return a.size()>b.size();
    for(int i=a.size()-1;i>=0;i--)
        if(a[i]!=b[i])
            return a[i]>b[i];
    return true;
}

vector<int> sub(vector<int>& a,vector<int>& b){
    vector<int> ans;
    int t=0;
    for(int i=0;i<a.size();i++){
        t=a[i]-t;
        if(i<b.size()) t-=b[i];
        ans.push_back((t+10)%10);
        if(t<0) t=1;
        else t=0;
    }
    while(ans.size()>1&&ans.back()==0) ans.pop_back();
    return ans;
}

int main(){
    string sa,sb;
    vector<int> a,b,ans;
    cin>>sa>>sb;
    for(int i=sa.length()-1;i>=0;i--) a.push_back(sa[i]-'0');
    for(int i=sb.length()-1;i>=0;i--) b.push_back(sb[i]-'0');
    if(cmp(a,b))
        ans=sub(a,b);
    else
        ans=sub(b,a),cout << '-';
    for(int i=ans.size()-1;i>=0;i--)
        cout << ans[i];
    cout << endl;
    return 0;
}

高精度乘法

例题

https://www.acwing.com/problem/content/795/

思路

高精度乘法

我们这里只考虑简单的情况：乘数中的一个是普通的 int 类型。有没有简单的处理方法呢？

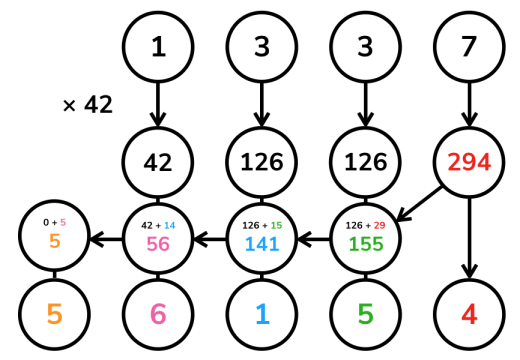
一个直观的思路是直接将$a$每一位上的数字乘以$b$。从数值上来说，这个方法是正确的，但它并不符合十进制表示法，因此需要将它重新整理成正常的样子。

重整的方式，也是从个位开始逐位向上处理进位。但是这里的进位可能非常大，甚至远大于$9$，因为每一位被乘上之后都可能达到$9b$的数量级。所以这里的进位不能再简单地进行$-10$运算，而是要通过除以$10$的商以及余数计算。可以参考下图展示的一个计算高精度数$1337$乘以单精度数$42$的过程。

模板

#include <iostream>
#include <vector>
using namespace std;

vector<int> mul(vector<int>& a,int b){
    vector<int> ans;
    int t=0;
    for(int i=0;i<a.size();i++){
        t+=a[i]*b;
        ans.push_back(t%10);
        t/=10;
    }
    while(t) ans.push_back(t%10),t/=10;
    return ans;
}

int main(){
    string s;
    vector<int> a;
    int b;
    cin>>s>>b;
    for(int i=s.length()-1;i>=0;i--)
        a.push_back(s[i]-'0');
    vector<int> ans=mul(a,b);
    for(int i=ans.size()-1;i>=0;i--)
        cout << ans[i];
    cout << endl;
    return 0;
}

高精度除法

例题

https://www.acwing.com/problem/content/796/

思路

高精度除法

竖式长除法实际上可以看作一个逐次减法的过程。例如上图中商数十位的计算可以这样理解：将$45$减去三次$12$后变得小于$12$，不能再减，故此位为$3$。

注意：由于除法与加减乘不同，是从高位到低位的计算顺序，所以我们在实现的函数中需要倒序遍历，而且返回答案的vector需要reverse一次，将顺序换回低到高

模板

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> div(vector<int>& a,int b,int &r){
    r=0;
    vector<int> ans;
    for(int i=a.size()-1;i>=0;i--){
        r=r*10+a[i];
        ans.push_back(r/b);
        r%=b;
    }
    reverse(ans.begin(),ans.end());
    while(ans.size()>1&&ans.back()==0)
        ans.pop_back();
    return ans;
}

int main(){
    string s;
    vector<int> a;
    int b,r;
    cin>>s>>b;
    for(int i=s.length()-1;i>=0;i--)
        a.push_back(s[i]-'0');
    vector<int> ans=div(a,b,r);
    for(int i=ans.size()-1;i>=0;i--)
        cout << ans[i];
    cout << endl << r << endl;
    return 0;
}

前缀和与差分

前缀和是一种重要的预处理，能大大降低查询的时间复杂度。我们可以简单理解为“数列的前 n 项的和”。

前缀和

例题

https://www.acwing.com/problem/content/797/

思路

对于这道题，我们有两种做法：

把对数组 A 的累加依次放入数组 B 中
递推： B[i] = B[i-1] + A[i] ，前提 B[0] = A[0]

注意：前缀和数组下标最好从1开始，不用处理边界问题

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int n,m,a[maxn],s[maxn];

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        s[i]=s[i-1]+a[i];
    int l,r;
    while(m--){
        scanf("%d%d",&l,&r);
        printf("%d\n",s[r]-s[l-1]);
    }
    return 0;
}

二维前缀和

例题

https://www.acwing.com/problem/content/798/

思路

前缀和几乎都是基于容斥原理

比如我们有这样一个矩阵 $a$ ，可以视为二维数组：

1
2
3

1 2 4 3
5 1 2 4
6 3 5 9

我们定义一个矩阵 $sum$ ， $sum_{x,y} = \sum\limits_{i=1}^x \sum\limits_{j=1}^y a_{i,j}$ ，
那么这个矩阵长这样：

1
2
3

1 3 7 10
6 9 15 22
12 18 29 45

第一个问题就是递推求 $sum$ 的过程， $sum_{i,j} = sum_{i - 1,j} + sum_{i,j - 1} - sum_{i - 1,j - 1} + a_{i,j}$ 。
因为加了 $sum_{i - 1,j}$ 和 $sum_{i,j - 1}$ 重复了 $sum_{i - 1,j - 1}$ ，所以减去。

第二个问题就是如何应用，譬如求 $(x1,y1) - (x2,y2)$ 子矩阵的和。
那么，根据类似的思考过程，易得答案为 $sum_{x2,y2} - sum_{x1 - 1,y2} - sum_{x2,y1 - 1} + sum_{x1 - 1,y1 - 1}$ 。

模板

#include <iostream>
#include <cstring>
using namespace std;
const int maxn=1010;

int a[maxn][maxn],n,m,q;

int main(){
    memset(a,0,sizeof(a));
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]),a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
    int x1,y1,x2,y2;
    while(q--){
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",a[x2][y2]-a[x1-1][y2]-a[x2][y1-1]+a[x1-1][y1-1]);
    }
    return 0;
}

差分

例题

https://www.acwing.com/problem/content/799/

思路

差分，是一种和前缀和相对的策略

差分是对相邻两数取差即$b_i=a_i-a_{i-1}$

然后我们不难证出对$b$数组求一遍前缀和就可以得到$a$数组了

它可以维护多次对序列的一个区间加上一个数，并在最后询问某一位的数或是多次询问某一位的数。（总之修改操作一定要在查询操作之前）

假设我们要对$[l,r]$区间每一个数都加上$x$，就进行$b_l = b_l + x,b_{r + 1} = b_{r + 1} - x$的操作就可以了，我们就可以将每次区间更新从$O(n)$的复杂度直接降成$O(1)$的复杂度，最后再执行一遍$O(n)$ 的求前缀和就可以还原调整后的数组了

我们在构造差分数组的时候其实也可以使用插入法构造（边读入边构造），使用模板中的insert函数即可

注意:差分数组最好也从下标1开始，避免处理边界

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn];

void insert(int l,int r,int x){
    a[l]+=x;
    a[r+1]-=x;
}

int main(){
    int n,m,l,r,x;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&x),insert(i,i,x);
    while(m--){
        scanf("%d%d%d",&l,&r,&x);
        insert(l,r,x);
    }
    for(int i=1;i<=n;i++){
        a[i]+=a[i-1];
        if(i>1) printf(" ");
        printf("%d",a[i]);
    }
    puts("");
    return 0;
}

二维差分

例题

https://www.acwing.com/problem/content/800/

思路

如同二维前缀和一样，二维差分也是运用容斥定理对一维的扩展

在$[l,r]$区间加上$x$的一维的差分公式是$b_l = b_l + x,b_{r + 1} = b_{r + 1} - x$

那么在二维的$(x1,y1),(x2,y2)$加上$val$的差分公式是

$a_{x1,y1} = a_{x1,y1} + val$

$a_{x2+1,y1} = a_{x2+1,y1} - val$

$a_{x1,y2+1} = a_{x1,y2+1} - val$

$a_{x2+1,y2+1} = a_{x2+1,y2+1} + val$

最后我们只需要对差分数组求前缀和就可以还原整个数组了

还是这个二维前缀构造公式：$a_{i,j} = a_{i,j} + a_{i-1,j} + a_{i,j-1} - a_{i-1,j-1}$

模板

#include <iostream>
using namespace std;
const int maxn=1010;

int a[maxn][maxn];

void insert(int x1,int y1,int x2,int y2,int val){
    a[x1][y1]+=val;
    a[x2+1][y1]-=val;
    a[x1][y2+1]-=val;
    a[x2+1][y2+1]+=val;
}

int main(){
    int n,m,q,val;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&val),insert(i,j,i,j,val);
    int x1,y1,x2,y2;
    while(q--){
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&val);
        insert(x1,y1,x2,y2,val);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
            if(j>1) printf(" ");
            printf("%d",a[i][j]);
        }
        printf("\n");
    }
    return 0;
}

双指针

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。双指针可以从不同的方向向中间逼近也可以朝着同一个方向遍历

下面是一般双指针问题的模板

由于双指针算法是一个灵活性很高的算法，所以模板只是个思路，具体问题还是需要具体考虑

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}
常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

最长连续不重复子序列

例题

https://www.acwing.com/problem/content/801/

思路

这是一个较为简单的双指针问题，首先我们的$i$指针一直从前往后遍历，然后使用哈希表计数，通过哈希表的条件限制将$j$指针向前移动，并随时更新答案

注意：$j$指针向前移动一直到新更新的$s[a[i]]$变为1为止，因为要确保数组没有重复，所以如果$s[a[i]] = 2$了，我们就要让$j$指针删除前面的那个重复数字

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn],s[maxn];

int main(){
    int n,ans=0;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    for(int i=0,j=0;i<n;i++){
        s[a[i]]++;
        while(j<=i&&s[a[i]]>1) s[a[j]]--,j++;
        ans=max(ans,i-j+1);
    }
    printf("%d\n",ans);
    return 0;
}

数组元素的目标和

例题

https://www.acwing.com/problem/content/802/

思路

首先$a$数组和$b$数组都是升序的数组这一点是非常关键的，也就是说假设$a[0] + b[m-1] > x$，那么$a[1] + b[m-1] > x$也是一定的，所以我们可以省略很多的不必要比较的数对，当$i$指针和$j$指针相加大于目标值就将$j$指针后退，保证下一个$a[i]$仍然有可能在解的范围内

模板

#include <iostream>
using namespace std;
const int maxn=1e5+10;

int a[maxn],b[maxn];

int main(){
    int n,m,x;
    scanf("%d%d%d",&n,&m,&x);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    for(int i=0;i<m;i++) scanf("%d",&b[i]);
    for(int i=0,j=m-1;i<n;i++){
        while(j>=0&&a[i]+b[j]>x) j--;
        if(a[i]+b[j]==x){
            printf("%d %d\n",i,j);
            break;
        }
    }
    return 0;
}

位运算

二进制中1的个数

例题

https://www.acwing.com/problem/content/803/

思路

这个题其实就是介绍了树状数组中要用到的一种lowbit运算，即快速地统计二进制中1的个数

int lowbit(int x) {
  //算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数
  return x & -x;
}

lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1，举个例子，x = 6，它的二进制为110，那么lowbit(x)就返回2。

求lowbit：

先消掉最后一位1，然后再用原数减去消掉最后一位1后的数，答案就是lowbit(x)的结果；
因为一个负数的补码的特点，我们把这个负数对应的正数与该负数相&，由于这个1的左边的二进制与正数的原码对应的部分是相反的，所以为0,；由于这个1和这个1右边的二进制都是不变的，因此，相与后还是原来的样子，这就是lowbit(x)的原理

模板

#include <iostream>
using namespace std;

int lowbit(int x){
    return x&(-x);
}

int main(){
    int n,x,ans;
    cin>>n;
    while(n--){
        cin>>x;
        ans=0;
        while(x) x-=lowbit(x),ans++;
        cout << ans << ' ';
    }
    cout << endl;
    return 0;
}

离散化

例题

https://www.acwing.com/problem/content/804/

思路

首先放上离散化的模板

vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r){
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}

这道题由于数轴无限长，所以如果直接开数组求根本开不出来，但是我们可以采用离散化的方式将数组空间压缩到$3e5$,然后就可以直接采用单点更新和前缀和的方式完成题目的要求了

注意：因为x,l,r三个变量需要进行离散化，每个变量大小是$1e5$，所以我们总共需要开$3e5$的大小

模板

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn=3e5+10;
typedef pair<int,int> P;

int a[maxn],s[maxn];
vector<int> v;
vector<P> add,query;

int getid(int x){
    return (int)(lower_bound(v.begin(),v.end(),x)-v.begin()+1);
}

int main(){
    int n,m,x,c,l,r;
    cin>>n>>m;
    for(int i=0;i<n;i++)
        cin>>x>>c,add.push_back({x,c}),v.push_back(x);
    for(int i=0;i<m;i++){
        cin>>l>>r,query.push_back({l,r});
        v.push_back(l);v.push_back(r);
    }
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    for(auto x:add)
        a[getid(x.first)]+=x.second;
    for(int i=1;i<=v.size();i++)
        s[i]=s[i-1]+a[i];
    for(auto x:query)
        cout << s[getid(x.second)]-s[getid(x.first)-1] << endl;
    return 0;
}

区间合并

区间合并问题

例题

https://www.acwing.com/problem/content/805/

思路

首先先放上模板

// 将所有存在交集的区间合并
void merge(vector<P> &segs)
{
    vector<P> res;
    sort(segs.begin(), segs.end());
    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first){
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);
    if (st != -2e9) res.push_back({st, ed});
    segs = res;
}

其实思路很简单，首先就是按照左端点排序，然后遍历，如果右端点超过了下一个区间的左端点，就将右端点更新成下一个区间的右端点，以此类推即可

模板

#include <iostream>
#include <algorithm>
#include <climits>
#include <vector>
using namespace std;
typedef pair<int,int> P;

vector<P> v;

void merge(vector<P>& v){
    vector<P> ans;
    sort(v.begin(),v.end());
    int l=INT_MIN,r=INT_MIN;
    for(auto x:v){
        if(r<x.first){
            if(l!=INT_MIN) ans.push_back({l,r});
            l=x.first,r=x.second;
        }
        else r=max(r,x.second);
    }
    if(l!=INT_MIN) ans.push_back({l,r});
    v=ans;
}

int main(){
    int n,l,r;
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>l>>r,v.push_back({l,r});
    merge(v);
    cout << v.size() << endl;
    return 0;
}