这次这篇文章主要是讨论一个经典的问题和一个经典的算法,首先我们可以看到这个问题叫做RMQ问题,然后我们接下来讨论的这个算法就是用来解决这个经典的问题的,由Tarjan大牛发明创造的Sparse-Table算法.
RMQ问题
先来说说RMQ问题,RMQ问题的全称叫做范围最值问题(Range Minimum/Maximum Query),是指这样一个问题:对于长度为n的数列A,回答若干次询问RMQ(i,j),返回数列A中下标在区间[i,j]中的最小/大值。
Sparse-Table算法(简称ST算法)
Tarjan大牛发明了很多知名的算法,Sparse-Table算法就是其中的一个,我们首先来讲一下这个算法的原理.
我们可以看到在RMQ问题中最浪费时间的就是一次接着一次的查询,如果查询次数多的话是非常浪费时间的,不过,既然我们每次查询的性质都一样的话(都是一个范围内求最值),我们可不可以经过一些预先的处理,将多次查询的复杂度降下来呢?
答案是可以的,我们完全可以这样做,我们原先是使用一维数组存数据,然后机械地去寻找最值,我们现在仍然还是使用这一维的数据,不过,我们可以建立另一个维度去存放关于最值的信息.假如我们最开始是使用d[i]去存储数据,但是我现在再开另一个维度使其变成d[i][j],我们使用d[i][0]存储原来的数据.
那么在j>0的数据中存什么呢,这就是关键了.当j=1,我们存储的就是两两之间的最值.当j=2时,我们存储的是四个四个之间的最值.当j=3时,我们存储每八个元素的最值.细心地同学已经可以发现了,就是2的j次方嘛!
所以我们可以用这种方法去保留最值,当然我们初始化的时候得使用一下动态规划,利用已经求出来的区间最值去求更大的区间最值.
1 | void init(const vector<int>& a){ |
接下来就是如何查询的问题了,查询的操作有一点抽象,建议同学们自己找一些例子去理解一下,不要干看.
如果我们要查询[L,R]的最大值,我们有已经初始化成功的d数组,我们首先得算出(R-L+1)介于2的几次方之间,然后取两个刚好比(R-L+1)小一个量级的维度2^k,如下图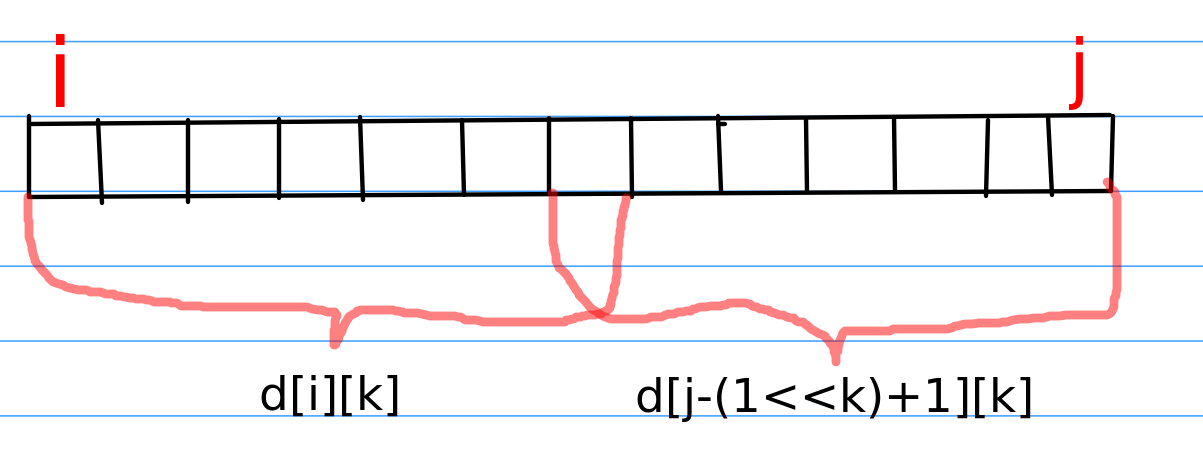
有人会担心重复覆盖的元素会影响结果,这个很显然是不会的.以下是代码:1
2
3
4
5
6
7
8int RMQ(int L,int R){
if(L>R)
return 0;
int k=0;
while((1<<(k+1))<=R-L+1)
k++;
return max(d[L][k],d[R-(1<<k)+1][k]);
}
一道题目(题目翻译来自洛谷)
题目传送门:https://www.luogu.org/problemnew/show/UVA11235
题目描述: 给出一个非降序排列的整数数组a1,a2,…,an,你的任务是对于一系列询问i,j,回答ai,ai+1,…aj中出现次数最多的值所出现的次数
输入数据: 输入包含多组数据。每组数据第一行为两个整数n和q(1≤n,q≤100000)。第二行包含n个非降序排列的整数a1,a2,…,an(-100000≤ai≤100000)。以下q行每行包含两个整数i和j(1≤i≤j≤n),输入结束标志为n=0
输出格式 对于每个查询i,j,输出查询结果,也就是i~j中出现次数最多的数的个数,之间用换行隔开
注:朴素算法可能会超时!(这个注释原本题目里面就有,不是我自己加的。。)
由 @hicc0305 提供翻译
分析
首先这道题乍看上去好像想不到RMQ问题上,不过仔细一想,如果我们提前把每个数出现的次数都统计下来放到一个数组里,不就等于每一次询问就是在求区间最大值吗?
但是这题目并不是统计一下然后跑一遍ST算法这么简单的,因为我们的题目的询问的位置很可能会在一串连续的向相同的数字中间,然后在外部的数字就不会被算进去,这时候我们根据元素值去进行ST算法后就会多算值,那就很糟糕了.
那么我们就要记忆每一串相同的数字的起始位置和终止位置,然后在我们使用ST算的时候最左边的那个元素和最右边的元素我们都不要使用ST算法去算(只有最左边的元素和最右边的元素可能会被截断),而是使用相对位置去算,然后中间的元素就可以使用正常的高效的ST算法运算,最后得到的三个结果取个最大值就可以了.
以下是AC代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
using namespace std;
const int maxn=100010;
struct Segment{
int val;
int cnt;
Segment(int val,int cnt):val(val),cnt(cnt){}
Segment():val(0),cnt(0){}
};
struct Loc{
int left;
int right;
int num;
Loc():left(0),right(0),num(0){}
};
int d[maxn][20];
void init(const Segment* a,int seg_num){
for(int i=0;i<seg_num;i++)
d[i][0]=a[i].cnt;
for(int j=1;(1<<j)<=seg_num;j++)
for(int i=0;i+(1<<j)-1<seg_num;i++)
d[i][j]=max(d[i][j-1],d[i+(1<<(j-1))][j-1]);
}
int RMQ(int L,int R){
if(L>R)
return 0;
int k=0;
while((1<<(k+1))<=R-L+1)
k++;
return max(d[L][k],d[R-(1<<k)+1][k]);
}
int main(){
ios::sync_with_stdio(false);
int n,q;
while(cin>>n&&n){
cin>>q;
int *s=new int[n+10];
Segment* seg=new Segment[n+10];
Loc* loc=new Loc[n+10];
for(int i=1;i<=n;i++)
cin>>s[i];
int count=1,seg_num=0;
for(int i=1;i<=n;i++){
while(s[i]==s[i+1]){
i++;
count++;
}
seg[seg_num].val=s[i];
seg[seg_num].cnt=count;
seg_num++;
count=1;
}
int num=1,left,right,f;
for(int i=0;i<seg_num;i++){
f=0;
while(s[num]==seg[i].val){
if(!f) {
left = num;
right= left+seg[i].cnt-1;
f=1;
}
loc[num].num=i;
loc[num].left=left;
loc[num].right=right;
num++;
}
}
init(seg,seg_num);
int a,b;
while(q--){
cin>>a>>b;
if(a>b)
swap(a,b);
if(loc[a].num==loc[b].num)
cout << b-a+1 << endl;
else
cout << max(loc[a].right-a+1,max(b-loc[b].left+1,RMQ(loc[a].num+1,loc[b].num-1))) << endl;
}
}
return 0;
}