这次这篇博客介绍的是ACM中一群非常有意思的题目，就是玩游戏。这种游戏题基本都使用了博弈论的知识，今天我们就来浅谈一下博弈论。

只讨论公平游戏

我们接下来讨论的问题，都有一些显著的特征。比如说，一个游戏者可以改变的状态或者进行的操作，另外一个游戏者一定也可以，而且游戏的道具基本都是双方所共有的，并没有五子棋或围棋里一个人拿黑子一个人拿白子的情况。

状态图

我们在解决博弈问题的时候，最好在草稿纸上记录后续的状态以及每个状态相互转化的关系，将转换关系画成一张图，我们就叫这个为状态图。状态图是我们解决博弈问题的利器，可以很直观地看到状态之间的关系然后找出规律。

必败状态和必胜状态

一般的ACM组合游戏题目都会假定双方都足够聪明，也就是双方的每一步都会选择最优解法，然后讨论双方的输赢，这样我们就会得到两种状态（有且只有两种）：必败状态和必胜状态。

首先，如果无法继续移动或操作的状态是必败状态，当然这也是终态。那么，如果我们在一个状态下可以进行一个操作，将这个状态转移到必败状态（这时候轮到对方了，对方处于必败状态那他就输定了），那么我们当前的这个状态一定就是必胜状态。再反过来想，如果我们处于一个状态，我们做所有种类的操作，都会把这个状态转移到必胜状态，那么我们现在所在上的就是必败状态，所以我们可以得出结论：
一个状态是必败状态当且仅当它的所有后继都是必胜状态
一个状态是必胜状态当且仅当它至少有一个后继是必败状态
没有后继状态的状态是必败状态（规则是不能操作的人就输了）

从Ferguson游戏开始

有两个盒子，一个有m颗糖一个有n颗糖，这样的状态记为(m,n)，每次的操作是将一个盒子清空然后把另一个盒子中的一部分糖拿到空盒子里去，使两个盒子始终保持至少有一颗糖，两个选手交替做这个操作，无法保持两个盒子有糖的状态的选手落败，另一个选手赢。求先手必败的状态。

我们把状态设定为(m,n)，我们首先就可以看出状态(1,1)是必败状态,那么我们可以倒着推，由于(1,1)是必败态，所以我们可以将所有能推出状态(1,1)的状态都设置成必胜状态。当然我们不能一下子就“大跃进”，所以我们需要一步一步“步步蚕食”。我们可以先列举m+n=3的所有情况，再列举m+n=4的所有情况（因为我们可以肯定m+n=4的情况需要m+n=3的情况来作判断）。这样我们就像递推一样能解决所有的情况。

#include <iostream>
using namespace std;
const int maxn = 100;

int main(){
    bool win[maxn][maxn];
    win[1][1]=false;
    for(int k=3;k<=20;k++){
        for(int n=1;n<k;n++){
            int m=k-n;
            win[n][m]=false;
            for(int i=1;i<n;i++)
                if(!win[i][n-i])
                    win[n][m]=true;
            for(int i=1;i<n;i++)
                if(!win[i][m-i])
                    win[n][m]=true;
        }
    }
    return 0;
}

巴什博弈（Bash Game）——hdu1846

接下来就是第一个博弈论知识——巴什博弈。场景是这样的：
只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

一开始看这题的时候很可能会一脸雾水，因为这个n和m我们都无法具象化，面对这个博弈我们该如何做呢？这时候我们就要借用上一个介绍的Ferguson游戏的思想了：我们可以找到状态图。找到状态图的关键就是先找到终态和必败态，既然所有的状态但是从终态推出来的，我们就先找到终态，再通过终态继续推进。

我们可以发现0是最终的状态（因为对手已经取完了），那么1到m所有的数字都是必胜态，这一条信息非常关键，因为我们立刻可以推出m+1一定是一个必败态（m+2就不行，因为我可以只拿一个，这样对手就变成了必败态），然后我们可以做一个操作，立刻催眠自己：m+1是一个终态（也可以认为m+1就是0），这样我们就可以同样推出m+2到2m+1都是必胜态（因为可以通过一步操作到达m+1），我们又可以神奇地推出2m+2就是必败态了，以此类推我们再将2m+2看作0，我们可以依据这些规律知道只要我们的物品符合m+1的倍数，先取的人一定必输，所以这题的代码就变得非常简单了

#include <iostream>
using namespace std;

int main(){
    int T,m,n;
    cin>>T;
        while(T--) {
            cin >> n >> m;
            if (n % (m + 1) == 0)
                cout << "second" << endl;
            else
                cout << "first" << endl;
        }
    return 0;
}

威佐夫博弈（Wythoff’s game）——hdu1527

有两堆石子，数量任意，可以不同。游戏开始由两个人轮流取石子。游戏规定，每次有两种不同的取法，一是可以在任意的一堆中取走任意多的石子；二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目，如果轮到你先取，假设双方都采取最好的策略，问最后你是胜者还是败者。

这种情况下是颇为复杂的。我们用（a[k]，b[k]）（a[k] ≤ b[k] ,k=0，1，2，…,n)（表示两堆物品的数量并称其为局势，如果甲面对（0，0），那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势是：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。注：k表示奇异局势的序号，第一个奇异局势k=0。

可以看出a[k]是在之前未出现过的最小自然数，而b[k] = a[k]+k，k代表出现的第几个奇异局势。我们就可以得出如下公式：a表示第一堆的个数，b表示第二堆的个数，n表示二者之差，a小于b，经过前人的找规律我们会得出这样的结果，a=n*1.618，

使用这样的规律我们就可以做hdu的1527题了，无非就是判断一下就可以了，在这道题中我们只需判断数据中的a和我们使用(int)(n*(1+sqrt(5))/2)算出来的a是不是相等，如果相等那么就是奇异局势，当然就是必败态了，如果不等那么就是必胜态。

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

int main(){
    int a,b;
    while(cin >> a >> b){
        if(a>b)
            swap(a,b);
        int n=b-a;
        if(a==(int)(n*(1+sqrt(5))/2))
            cout << 0 << endl;
        else
            cout << 1 << endl;
    }
    return 0;
}

斐波那契博弈（Fibonacci Nim）——hdu2516jian

1堆石子有n个,两人轮流取.先取者第1次可以取任意多个，但不能全部取完.以后每次取的石子数不能超过上次取子数的2倍。取完者胜.先取者负输出”Second win”.先取者胜输出”First win”。

这个和之前的巴什博弈和威佐夫博弈有一个很大的不同点，就是游戏规则的动态化。之前的规则中，每次可以取的东西的策略是基本固定的，但是这次有规则2：一方每次可以取的东西的数目依赖于对手刚才取的数量。

结论：当n为Fibonacci数的时候，先手是必败状态。

这里的证明使用了数学归纳法，具体的步骤我就不多打了，可以移步至这篇文章：https://blog.csdn.net/dgq8211/article/details/7602807

所以这道题我们只需要提前将斐波那契数计算出来，打表即可

#include <iostream>
using namespace std;

int main(){
    int n;
    int fib[50];
    fib[1]=1;fib[2]=1;
    for(int i=3;i<=47;i++)
        fib[i]=fib[i-1]+fib[i-2];
    while(cin>>n&&n){
        int flag=0;
        for(int i=1;i<=47;i++){
            if(n==fib[i]) {
                flag = 1;
                break;
            }
        }
        if(flag)
            cout << "Second win"  << endl;
        else
            cout << "First win" << endl;
    }
    return 0;
}

Nim博弈——hdu1850

下面是一个二人小游戏：桌子上有M堆扑克牌；每堆牌的数量分别为Ni(i=1…M)；两人轮流进行；每走一步可以任意选择一堆并取走其中的任意张牌；桌子上的扑克全部取光，则游戏结束；最后一次取牌的人为胜者。
现在我们不想研究到底先手为胜还是为负，我只想问大家：——“先手的人如果想赢，第一步有几种选择呢？”

假如是是2堆或者3堆甚至4堆的话，我们完全可以通过枚举状态的做法来解决这个问题，可是这道题的堆数有点多，肯定不可以这么做了，我们又要借用前人留下来的一些经典的定理了。

下面介绍的这个定理是由L.Bouton在1902年提出的一个定理，状态(x1,x2,x3)为必败状态当且仅当x1 xor x2 xor x3=0（就是x1^x2^x3=0），这里的xor就是异或操作，这种x1^x2^x3的结果也称为Nim和，当然如果是四个或者五个甚至n个，都可以用一直异或的操作算出答案比较是否为0来解决。

我们接下来给出这个定理的证明（借鉴了《算法竞赛入门经典》的证明）：
首先我们需要证明两条经典定理：1.一个状态是必败状态当且仅当它的所有后继都是必胜状态。2.一个状态是必胜状态当且仅当它至少有一个后继是必败状态。

首先是第一条：
对于一个多次异或答案能为0的一组数字，假设是x1,x2,x3，我们不管改变哪一个数字的哪一位（因为一次只能操作一堆牌，所以不可能同时改变很多位），肯定都可以使答案中多产生一个1，那么我们就证明了一个状态是必败状态当且仅当它的所有后继都是必胜状态。

然后是第二条：
我们还是假设为x1,x2,x3三堆火柴，假设我们算出了x1和x2的值，我们要对x3做操作使得这三堆异或为0，我们可以将x3变成（x2^x1），这样整个式子就变成了x1^x2^(x2^x1)，熟悉异或计算就可以瞬间得出答案为0。这样我们就成功地证明了一个状态是必胜状态当且仅当它至少有一个后继是必败状态。

这样我们就成功地证明了这个定理可以准确的适用于Nim博弈，根据这个定理的思想，这道题的代码也非常简单（话说博弈论的代码都比较简单）

#include <iostream>
using namespace std;

int main(){
    int m,x,ans;
    int a[110];
    while(cin>>m&&m){
        x=0;ans=0;
        for(int i=0;i<m;i++) {
            cin >> a[i];
            x^=a[i];
        }
        if(x==0)
            cout << 0 << endl;
        else{
            for(int i=0;i<m;i++){
                int pick=x^a[i];
                if(pick<a[i])
                    ans++;
            }
            cout << ans << endl;
        }
    }
    return 0;
}

阶梯博弈（Staircase Nim）——poj1704

从左到右有一排石子，给出石子所在的位置。规定每个石子只能向左移动，且不能跨过前面的石子。最左边的石子最多只能移动到1位置。每次选择一个石子按规则向左移动，问先手是否能赢。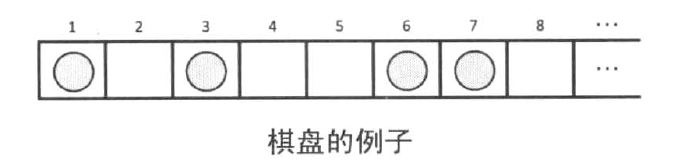

我们可以将这个博弈转化为Nim来做，我们先考虑棋子为偶数的情况，我们将棋子两两组成一对，我们可以把两个石子的距离看成Nim博弈中的一堆石子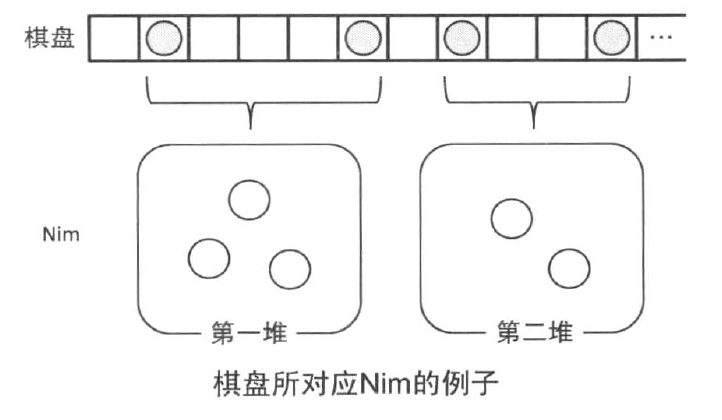

如果我们移动右边的石子，相当于从Nim的某一堆石子中取出石子，如下图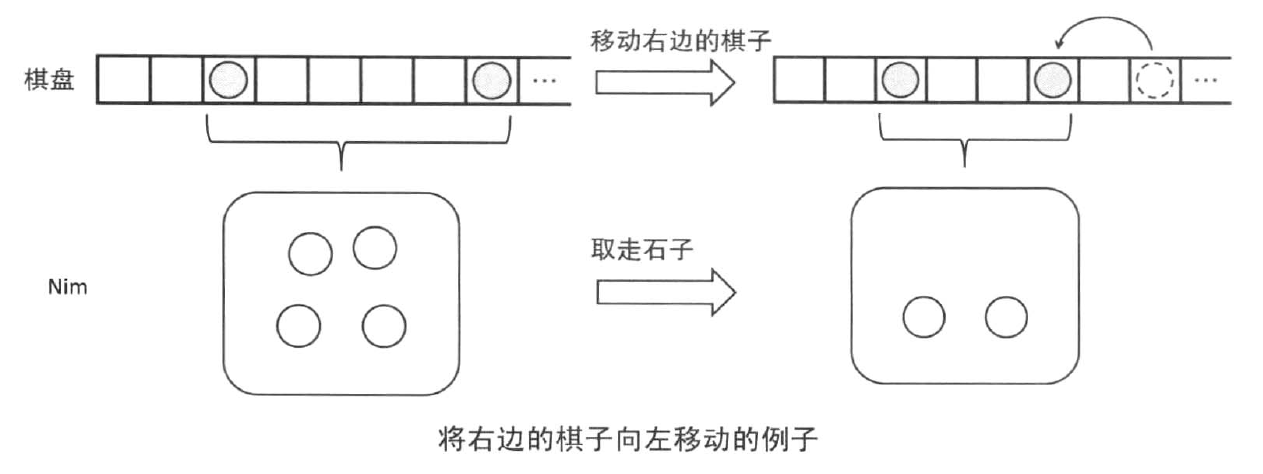

那就有一个问题了，如果我们想移动左边的石子，不就相当于增加石子了吗？Nim中又没有允许这一种操作。其实，这个问题并不关键，因为每个石子都没有移动步数的限制（除了在它左边的石子挡住它以外），这样我们完全可以假定右边的石子继续移动时会把左边石子增加的距离给补回来。这样这个问题就是一个Nim问题了。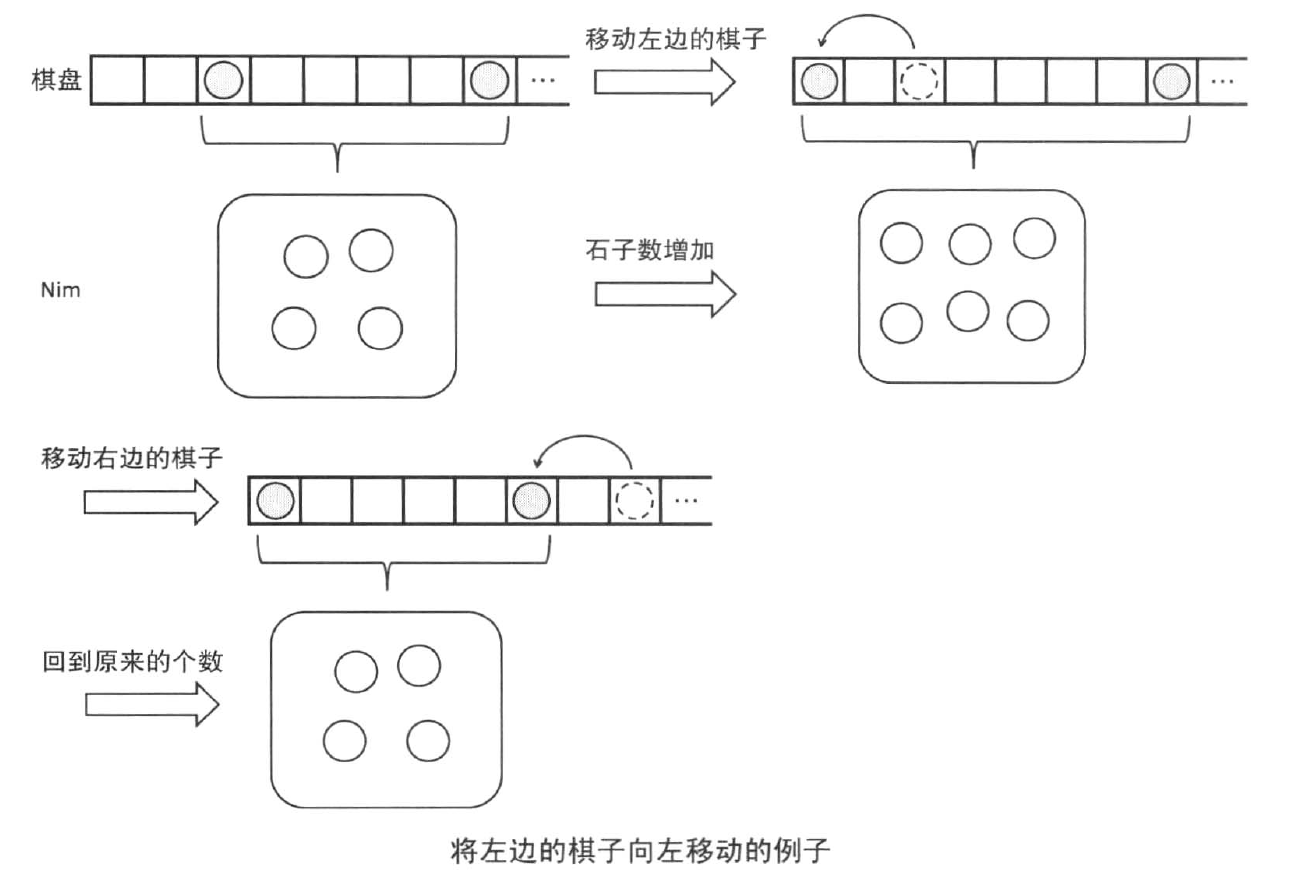

最后我们再来考虑一下奇数的情况，其实操作非常简单，我们只要在最前面的位置补上一个石子就可以了，假装是偶数。。。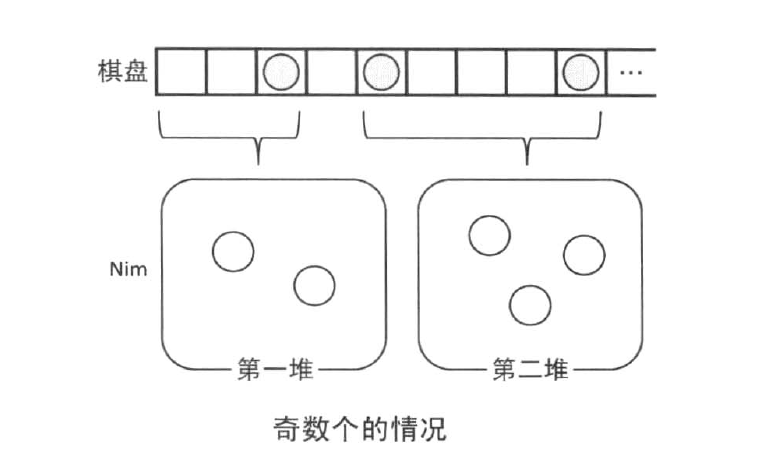

以上的示意图来自于《挑战程序设计竞赛》
下面是poj1704的代码

#include <iostream>
#include <algorithm>
using namespace std;

int main(){
    int T;
    while(cin>>T){
        int n;
        while(T--){
            cin >> n;
            int *a=new int[n+10];
            for(int i=0;i<n;i++)
                cin>>a[i];
            if(n%2)
                a[n++]=0;
            sort(a,a+n);
            int ans=0;
            for(int i=0;i<n-1;i+=2)
                ans^=(a[i+1]-a[i]-1);
            if(ans==0)
                cout << "Bob will win" << endl;
            else
                cout << "Georgia will win" << endl;
        }
    }
    return 0;
}

SG函数——hdu1847

大学英语四级考试就要来临了，你是不是在紧张的复习？也许紧张得连短学期的ACM都没工夫练习了，反正我知道的Kiki和Cici都是如此。当然，作为在考场浸润了十几载的当代大学生，Kiki和Cici更懂得考前的放松，所谓“张弛有道”就是这个意思。这不，Kiki和Cici在每天晚上休息之前都要玩一会儿扑克牌以放松神经。
“升级”？“双扣”？“红五”？还是“斗地主”？
当然都不是！那多俗啊~
作为计算机学院的学生，Kiki和Cici打牌的时候可没忘记专业，她们打牌的规则是这样的：
1、总共n张牌;
2、双方轮流抓牌；
3、每人每次抓牌的个数只能是2的幂次（即：1，2，4，8，16…）
4、抓完牌，胜负结果也出来了：最后抓完牌的人为胜者；
假设Kiki和Cici都是足够聪明（其实不用假设，哪有不聪明的学生~），并且每次都是Kiki先抓牌，请问谁能赢呢？
当然，打牌无论谁赢都问题不大，重要的是马上到来的CET-4能有好的状态。
Good luck in CET-4 everybody!

这个题目很有意思啊，我也快要考四级了哈哈哈。

要讨论SG函数，我们需要首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3，mex{1,3,5}=0，mex{}=0。

定义了mex运算，我们给出Sprague-Grundy函数的定义，我们将SG函数简写为g，定义：g(x)=mex{ g(y) | y是x的后继 }。

【实例】取石子问题

有1堆n个的石子，每次只能取{ 1, 3, 4 }个石子，先取完石子者胜利，那么各个数的SG值为多少？

SG[0]=0，f[]={1,3,4},

x=1 时，可以取走1 - f{1}个石子，剩余{0}个，所以 SG[1] = mex{ SG[0] }= mex{0} = 1;
x=2 时，可以取走2 - f{1}个石子，剩余{1}个，所以 SG[2] = mex{ SG[1] }= mex{1} = 0;
x=3 时，可以取走3 - f{1,3}个石子，剩余{2,0}个，所以 SG[3] = mex{SG[2],SG[0]} = mex{0,0} =1;
x=4 时，可以取走4- f{1,3,4}个石子，剩余{3,1,0}个，所以 SG[4] = mex{SG[3],SG[1],SG[0]} = mex{1,1,0} = 2;
x=5 时，可以取走5 - f{1,3,4}个石子，剩余{4,2,1}个，所以SG[5] = mex{SG[4],SG[2],SG[1]} =mex{2,0,1} = 3;

以此类推…..

我们算出SG函数有什么用呢？其实，SG函数就是将很多千奇百怪的博弈问题转化为Nim的关键工具，只要SG函数值等于0就相当于Nim中的必败状态，只要SG函数值不等于0就相当于Nim中的必胜状态。所以我们可以通过递推计算SG函数打表解出这道题。

#include <iostream>
#include <cstring>
using namespace std;
const int N=1005;

int main(){
    int vis[N];
    int sg[N];
    sg[0]=0;sg[1]=1;;
    for(int i=2;i<N;i++){
        memset(vis,0, sizeof(vis));
        for(int j=1;j<=i;j*=2)
            vis[sg[i-j]]=1;
        for(int j=0;;j++){
            if(!vis[j]){
                sg[i]=j;
                break;
            }
        }
    }
    int n;
    while(cin>>n){
        if(sg[n]==0)
            cout << "Cici" << endl;
        else
            cout << "Kiki" << endl;
    }
    return 0;
}

SG函数分治——hdu1848

任何一个大学生对菲波那契数列(Fibonacci numbers)应该都不会陌生，它是这样定义的：
F(1)=1;
F(2)=2;
F(n)=F(n-1)+F(n-2)(n>=3);
所以，1,2,3,5,8,13……就是菲波那契数列。
在HDOJ上有不少相关的题目，比如1005 Fibonacci again就是曾经的浙江省赛题。
今天，又一个关于Fibonacci的题目出现了，它是一个小游戏，定义如下：
1、这是一个二人游戏;
2、一共有3堆石子，数量分别是m, n, p个；
3、两人轮流走;
4、每走一步可以选择任意一堆石子，然后取走f个；
5、 f只能是菲波那契数列中的元素（即每次只能取1，2，3，5，8…等数量）；
6、最先取光所有石子的人为胜者；
假设双方都使用最优策略，请判断先手的人会赢还是后手的人会赢。

SG函数的威力远远不止于刚才那道题所展示的那样，SG函数解决有很多堆的博弈问题非常简单，这里放出一个威力巨大的定理：游戏和的SG函数等于各个游戏SG函数的Nim和。这意味着什么呢？也就是说：游戏的和的SG函数值是它的所有子游戏的SG函数值的异或。所以我们只要对上述的m,n,p这三堆石子都求一遍SG值，假设SG[m]=a,SG[n]=b,SG[p]=c，我们可以知道最后答案的SG值就是a^b^c,然后我们只要判断a^b^c是否等于0就可以解决这个问题了。

所以，对于我们来说，SG函数与“游戏的和”的概念不是让我们去组合、制造稀奇古怪的游戏，而是把遇到的看上去有些复杂的游戏试图分成若干个子游戏，对于每个比原游戏简化很多的子游戏找出它的SG函数，然后全部异或起来就得到了原游戏的SG函数，就可以解决原游戏了。你是否喜欢这个干净利落的SG函数呢？

还有就是这道题求SG函数的时候需要用到斐波那契数列，我们要提前算出来。下面是这道题的代码：

#include <iostream>
#include <cstring>
using namespace std;
const int N=1005;

int main(){
    int fib[30],sg[N],vis[N];
    fib[0]=fib[1]=1;
    for(int i=2;i<=25;i++)
        fib[i]=fib[i-1]+fib[i-2];
    sg[0]=0;sg[1]=1;
    for(int i=2;i<N;i++){
        memset(vis,0,sizeof(vis));
        for(int j=0;fib[j]<=i;j++)
            vis[sg[i-fib[j]]]=1;
        for(int j=0;;j++){
            if(!vis[j]){
                sg[i]=j;
                break;
            }
        }
    }
    int a,b,c;
    while(cin>>a>>b>>c&&(a||b||c)){
        int ans=sg[a]^sg[b]^sg[c];
        if(ans)
            cout << "Fibo" << endl;
        else
            cout << "Nacci" << endl;
    }
    return 0;
}

好了，到此为止很多常见的博弈论题型都已经介绍完了，如果你看到了这里，何不找你的小伙伴试一下这些博弈游戏和算法呢？
我们下一篇见！

In The End

组合游戏与博弈论