今天我们的主题是一个几何的小知识点——极角排序。

关于极角

先来解释一下极角吧。

我们首先来看一下最普通的直角坐标系下的角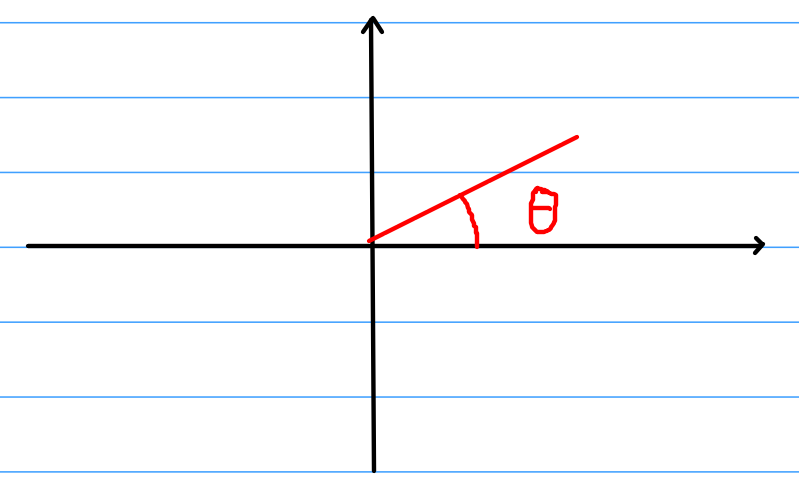

试想一下，我们将直角坐标换成极坐标，那么就会是这个样子的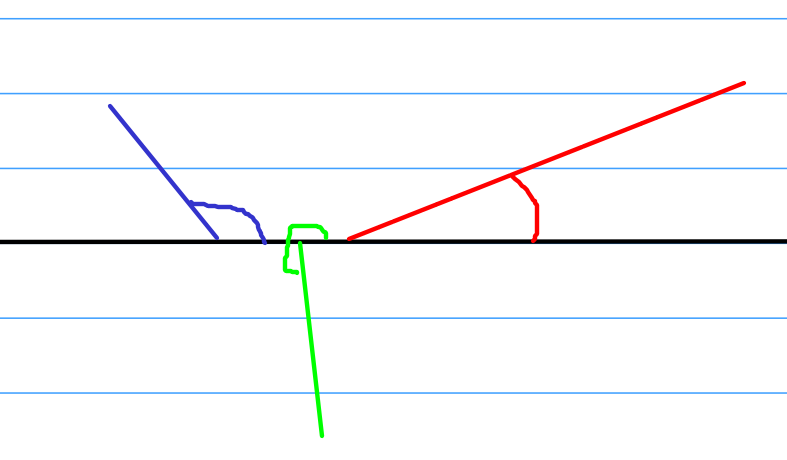

所以，我们先确定一条射线，然后我们就可以得出所有直线跟这条射线的夹角，我们可以将这种方式看作是直角坐标系被拿掉了y轴。

我们也可以规定逆时针为正或者是顺时针为正，当然我们习惯逆时针，因为直角坐标系就一直是这样的。

极角排序

顾名思义，就是按照极角大小的排序，我们假设平面上有很多个点，以一个点为轴，做一条水平线，然后我们就可以算出其他点和这个点连线的极角，然后我们根据极角来排序。如下图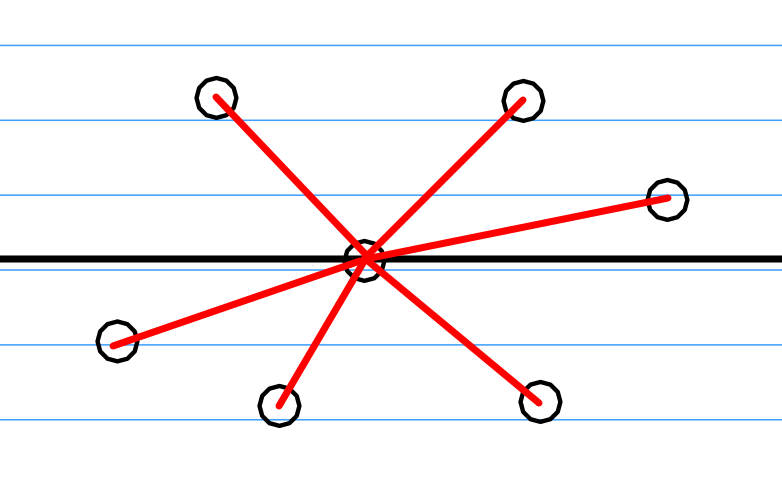

我们的目标就是以逆时针进行排序。我们有两种办法来解决。在此之前我们先定义好存储点坐标的结构体

struct point{
    double x;
    double y;
    point(double x=0, double y=0):x(x),y(y){}
};

atan2函数（在cmath头文件中）

1、atan（x）表示求的是x的反正切，其返回值为[-pi/2,+pi/2]之间的一个数。
2、atan2（y，x）求的是y/x的反正切，其返回值为[-pi,+pi]之间的一个数。

我们可以知道，通过反正切就可以求出直线与x轴的夹角了，所以我们就有了下面的代码（注意atan2函数的参数是先y再x，正好反一下）

bool compare(point a,point b){
    if(atan2(a.y,a.x)!=atan2(b.y,b.x))
        return atan2(a.y,a.x)<atan2(b.y,b.x);
    else return a.x<b.x;
}

二维叉积

相信很多人都已经接触过线代中的三维叉积了吧，接下来我们要介绍的工具叫做二维叉积，二维叉积在极角排序中也是真重要的一个求解方法。

例如： a=（x1,y1）,b=(x2,y2)
则 a×b=x1y2-x2y1

那么我们得到axb有什么用呢，这里可以通过公式推导出这么一个结果

那么我们就可以得到向量之间的位置关系了，这样就可以顺利地排序了，代码如下

double cross(point a,point b,point c,point d) {
    return (b.x - a.x)*(d.y - c.y) - (b.y - a.y)*(d.x - c.x);
}
bool compare(point a, point b) {
    return cross(point(), a, point(), b) >= 0;
}

总结

atan2在刷题的时候速度快，但是精度不佳
使用二维叉积不会被卡精度，但是速度略慢

请大家使用时看清楚题目在选择最合适的方法。