In The End

个人博客

0%

贪心算法：区间相关问题

发表于 更新于 分类于 ，

贪心算法与区间问题

这次跟前一篇文章一样，也是三道题，都是关于区间相交问题的。所谓区间问题，就是一个覆盖范围，那么要在一定条件下保证覆盖范围不重叠，这也是一个很有意思的问题。

选择不相交区间

首先我们研究的第一个问题就是如何在一众区间中选择尽量多的不相交的区间，我特意找到了我很久以前做过的一道题（那时候还没有这么系统地学习算法），就是HDU的2037题，题目叫“今年暑假不AC”（哈哈），相信有很多通过HDU11页开始ACM之旅的同学可能也做过，那我们就来重新温习一下。

首先贴出传送门：http://acm.hdu.edu.cn/showproblem.php?pid=2037
我下面也将整道题目复制了过来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Problem Description
“今年暑假不AC？”
“是的。”
“那你干什么呢？”
“看世界杯呀，笨蛋！”
“@#$%^&*%...”

确实如此，世界杯来了，球迷的节日也来了，估计很多ACMer也会抛开电脑，奔向电视了。
作为球迷，一定想看尽量多的完整的比赛，当然，作为新时代的好青年，你一定还会看一些其它的节目，比如新闻联播（永远不要忘记关心国家大事）、非常6+7、超级女生，以及王小丫的《开心辞典》等等，假设你已经知道了所有你喜欢看的电视节目的转播时间表，你会合理安排吗？（目标是能看尽量多的完整节目）
 
Input
输入数据包含多个测试实例，每个测试实例的第一行只有一个整数n(n<=100)，表示你喜欢看的节目的总数，然后是n行数据，每行包括两个数据Ti_s,Ti_e (1<=i<=n)，分别表示第i个节目的开始和结束时间，为了简化问题，每个时间都用一个正整数表示。n=0表示输入结束，不做处理。
 
Output
对于每个测试实例，输出能完整看到的电视节目的个数，每个测试实例的输出占一行。
 
Sample Input
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0

Sample Output
5

很多人可能第一时间会想到的就是排序，有些人会说对区间长度进行排序，有些人会说根据左端点进行排序，有些人会说对于右端点进行排序。那么究竟哪一种贪心的方案才是对的呢？我希望你看到这里可以自己动脑思考一下，或者是拿起笔自己画一下，又或者你可以机智地想出其他的贪心方案，那就尝试写出代码到HDU上提交看看能不能AC。总之，先请独立思考后再看下面的部分。

好的，那我就来分析一下这三种贪心方案的正确性。

1.对长度贪心
这种方案我觉得还是比较容易举出反例的，比如我下面画的这张图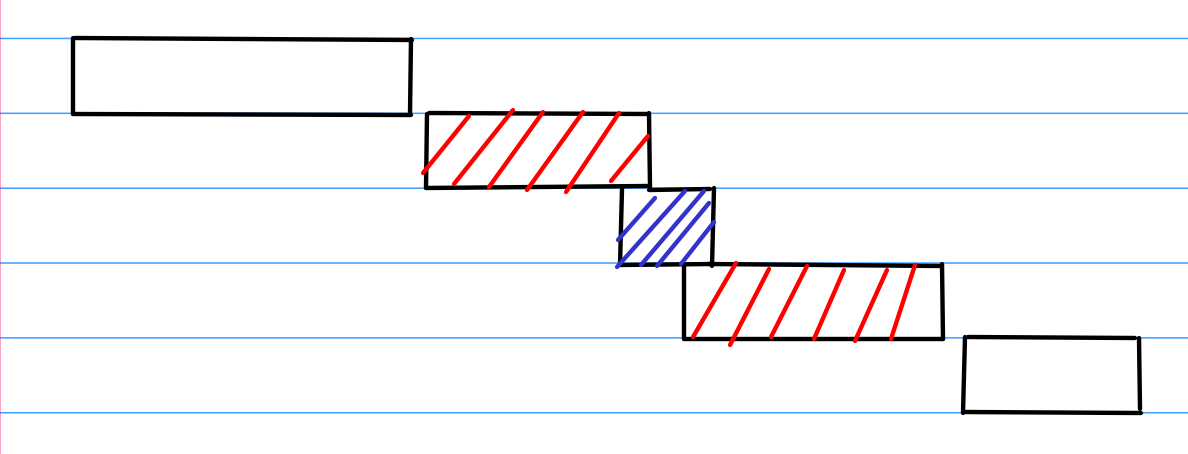

我们可以轻松的看出最中间的区间，虽然它短但是它同时破坏了两个区间，所以我们对长度贪心并不能得出正确答案。

2.对左端点贪心
那么假设我们对左端点贪心呢，我们把左端点从小到大排序可行吗？我觉得这种可能是最容易看出来的了，比如下图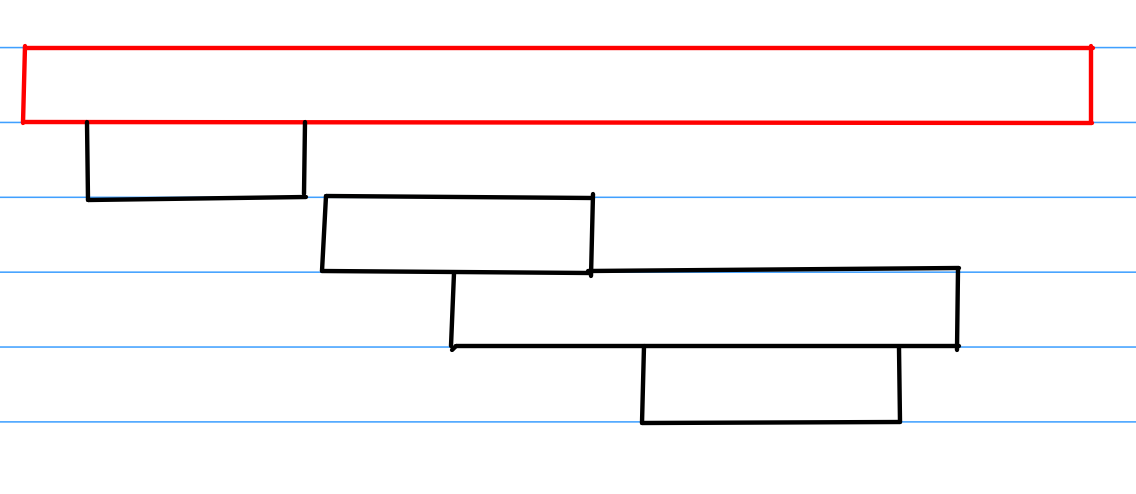

最左边这块完美地把所有区间抹杀了，所以这样贪心也是不行的。

3.对右端点贪心
很庆幸我们终于找到了正确的方法，可以在纸上自己画一下，我们会惊讶的发现用右端点排序得出的第一个区间永远是可选的，而且，右端点排序的贪心还非常方便，我们只需判断三种情况，就是相交的，分离的和包含的，首先分离的最好判断（直接选上不就完了），其次是包含的，我们肯定选择被包含的区间，因为被包含的区间更小，更能为后续的区间省空间，然后是相交的，我们只要按照右端点从小到大的顺序就可以完全避开纠结的过程（相交直接排除就可以了）。

其实关于上述的右端点排序为什么正确，语言上真的很难描述清楚，但是我绞尽脑汁想到了一个不太靠谱的证明：为什么左端点枚举错了但右端点却是对的呢？原因可能在于右端点枚举的特性，我们以最小的右端点为例，这个右端点就像一个通行站，别的区间的左端点可以通过它向外延伸，但是如果有别的区间的右端点全部都在它的右边，这就意味着别的区间永远会有这么一段（不管多短）永远在它的右边，所以它所在的区间永远比别的靠左。

这个东西需要比较强的理解能力，希望大家能积极思考。下面是AC代码，代码还是相当简单的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int,int> P;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n&&n){
        P* a=new P[n+10];
        for(int i=0;i<n;i++)
            cin>>a[i].first>>a[i].second;
        sort(a,a+n,[](P A,P B){return A.second<B.second;});
        int s=a[0].second,ans=1;
        for(int i=1;i<n;i++){
            if(s<=a[i].first){
                s=a[i].second;
                ans++;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

区间选点问题

数轴上有n个闭区间，去最少的点，使每个区间内至少都包含一个点（不同区间内含的点可以是同一个）

我们可以采用上一题的思路，只不过我们要小小地采取一点变化。我们每次在一个区间内放小球就直接放在最右边，因为整个区间是按照右端点排序的，所以，我们只需排除那些不需要放球的区间就可以知道要放多少球了，搞懂了上一题这题就非常简单了，而且代码也只需要修改一处即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int,int> P;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n&&n){
        P* a=new P[n+10];
        for(int i=0;i<n;i++)
            cin>>a[i].first>>a[i].second;
        sort(a,a+n,[](P A,P B){return A.second<B.second;});
        int s=a[0].second,ans=1;
        for(int i=1;i<n;i++){
            if(a[i].first>s){//只需要改动一下条件即可
                ans++;
                s=a[i].second;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

区间覆盖问题

数轴上有n个闭区间[a,b]。然后我们会得到一个指定的范围[s,t]，我们要选出最少的区间来完全覆盖这个指定的范围（需要判断无解的情况）。

首先我认为这是这次的三道题里面最麻烦的一道（我自己做这题的时间也是第三题比前面两题慢一些），但是做完之后其实我觉得思路还是蛮清晰的，就是一些细节的地方需要处理得比较细致。

首先紫书上有一个非常好的办法，先用左端点排序（注意这次不是右端点了），对在[s,t]范围以外所有区间直接不予考虑，然后修建在[s,t]中的区间的范围，例如左端点小于s的变成s，右端点大于t变成t，这样就非常简洁明了了。后面的步骤我是这样想的，既然修建了区间，那我就找最左边的区间（假设区间是[s,x]），那么完全可以将答案+1然后将所求区间变成[x+1，t]，然后我们重复利用上面的修剪过程，最后知道所求区间不断缩小到0，或者是找不到区间来填充输出“无解”。

过程仍需大家用心体会，我这里先把代码放上来了，我自己测试没有出什么问题，如果有错误请在下方评论区指出或给出错误数据，谢谢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int,int> P;
int n,s,t,ans;
P p[1000];

//修剪区间函数，注意left是引用，不然做不到修剪的效果
bool cut(int& left,int s,int t){
    int count=0;
    bool flag= false;
    for(int it=left;it<n;it++){
        //直接删除超范围的
        if(p[it].second<s)
            left++,count++;
        else if(p[it].first>t)
            break;
        else{//对于有一部分在范围内的区间，直接将范围外的部分剪掉
            flag=true;
            count++;
            if(p[it].first<s)
                p[it].first=s;
            if(p[it].second>t)
                p[it].second=t;
        }
    }
    return flag;
}

void sol(){
    //首先对左端点进行排序（因为我们后续是对左端点进行迭代）
    sort(p,p+n,[](P A,P B){return A.first<B.first;});
    //我只选择修剪了左端，其实右端也可以修剪，但是我嫌麻烦没加上去
    int left=0;
    if(!cut(left,s,t)){
        cout << "无解" << endl;
        return;
    }
    //因为一开始没+1出了一些bug
    int k=p[left].second+1;
    ans=1;
    while(k<=t){//后面就是对范围的不断填充，k越来越靠近t
        if(!cut(left,k,t)){
            cout << "无解" << endl;
            return;
        }
        k=p[left].second+1;
        ans++;
    }
    cout << "需要" << ans << "个区间" << endl;
}

int main(){
    ios::sync_with_stdio(false);
    while(cin>>n&&n){
        memset(p,0,sizeof(p));
        for(int i=0;i<n;i++)
            cin >> p[i].first >> p[i].second;
        cout << "输入线段范围：";
        cin>>s>>t;
        sol();
    }
    return 0;
}

OK，那么贪心算法与区间的问题也搞定了，下一篇应该就是哈夫曼编码了。