今天我们来接触一个有趣的几何问题，主角是一群蚂蚁

题意

首先我们给出传送门：https://vjudge.net/problem/UVA-1411

这个题目大概是这个意思：有n只蚂蚁和n棵苹果树，这n只蚂蚁想去吃苹果，蚂蚁和苹果树是一一对应的（卧槽，这么可怕！），一只蚂蚁只能上一棵树，一棵树上也只能有一只蚂蚁，然后题目会给出n个蚂蚁和n个树的位置，你要规划出哪只蚂蚁对应哪棵树，蚂蚁的行走路线必须是直线。当然没有这么简单，最重要的条件是，蚂蚁的行走路线不能相交。

不能相交这个条件就非常地烧脑了，首先我们必须建立一个比较合理地选取点的规则，不然到最后我们可能会算出一团乱麻，所以，怎么保证现在选取的路线不会使以后的蚂蚁无路可走，这是一个核心问题。

分析

首先这是一道分治的题目，那就更加提示了我们这道题具有普遍性的规律。那我们可以想到，一条路线是有什么组成的？就是一只蚂蚁和一棵树，那么假设我们迭代蚂蚁作为出发点，将对面的树作为可选择的选项，这样的模式似乎是可行的。好，那我们看似找到了一点方向。

但是我们换个角度思考，对于路线不重叠，重要的并不再是蚂蚁或者树谁找谁这个问题了，而是在于平面上的位置，正如我的标题所讲这是一道几何题，题目给的数据也是几何数据，所以我们必须使用几何的知识来解决问题。

我们可以自己在纸上模拟一下匹配，会发现一个比较有意思的事情。有两种情况的连线你一定有把握：
1.这条线在最边缘，根本没有分割平面内的其他点（就是其他点都在这条线的一个方向上），那么我连接这条线对其他的点根本就没影响嘛！下图就是这种情况。

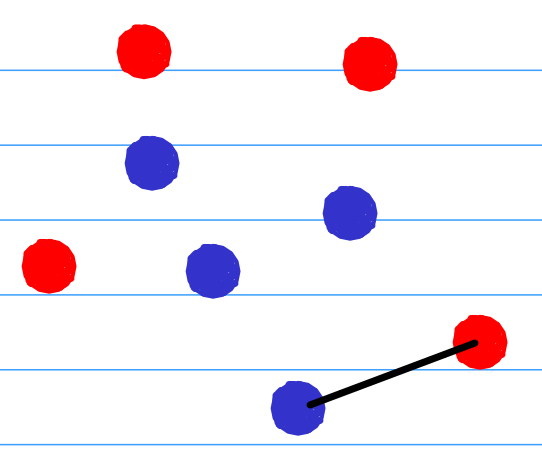
2.这条线分割了平面上的点，但是有趣的是，它分割得非常“优美”，它两个方向上的蚂蚁和树的数量都是相等的，就像下图这样。

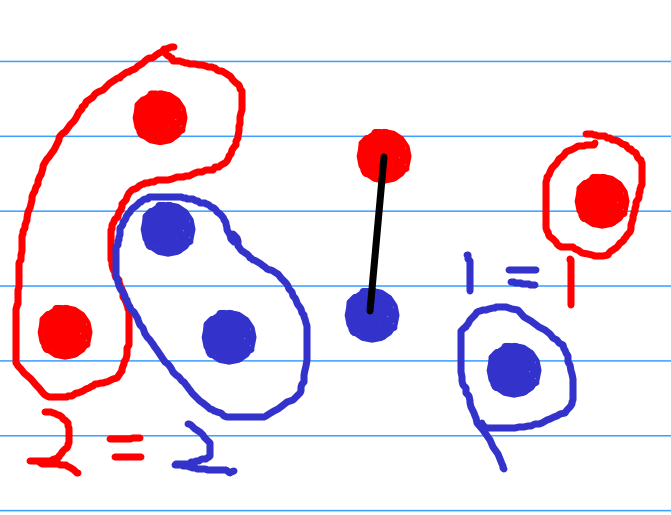
所以，我们就有了方案，我们可以利用这两种情况进行分治，我们再品味一下这一种算法会发现，其实第一种也算是第二种情况，因为0==0并非不可以啊，所以，我们也把第一种省略了。

然后我们可以选取一个固定的锚点，算法设计入门经典是选取了最下面的点（因为最方便计算sin角，使范围缩到0°-180°），然后我们通过计算sin角可以算出相应的位置，我们就从与x轴0角度开始扫向与x轴180度，然后对我经过的点进行计数，一旦发现线条左边和右边相等就可以配对了。

需要注意一点，我们会定义两个变量来对树和蚂蚁进行计数，千万不要忘记要将锚点算进去。意思就是假设锚点是蚂蚁，那么蚂蚁的数量一开始就是1，而树的数量一开始是0；假设锚点是树，那么树的数量一开始就是1了，蚂蚁则是0。这一点非常关键，否则无法进行计算。

代码

#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;

struct Point{
    int x,y;
    int num,color;
    double tilt;
}p[300];
int ans[300];

double cal(Point s,Point a){
    return (a.x-s.x)/sqrt((a.x-s.x)*(a.x-s.x)+(a.y-s.y)*(a.y-s.y));
}

void divide(int left,int right){
    if(left+1>=right)
        return;
    //先找出最下方的点
    sort(p+left,p+right,[](Point A,Point B){return A.y==B.y?A.x<B.x:A.y<B.y;});
    int color=p[left].color;
    for(int i=left+1;i<right;i++)
        p[i].tilt=cal(p[left],p[i]);
    //然后扇形状扫描
    sort(p+left+1,p+right,[](Point A,Point B){return A.tilt>B.tilt;});
    //起始点要设置好
    int s1=1,s2=0;
    for(int i=left+1;i<right;i++){
        if(p[i].color==color)
            s1++;
        else
            s2++;
        if(s1==s2){
            if(color==0)
                ans[p[left].num]=p[i].num;
            else
                ans[p[i].num]=p[left].num;
            divide(left+1,i);
            divide(i+1,right);
            break;
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    for(int cas=0;cin>>n;cas++){
        if(cas)
            cout << endl;
        for(int i=0;i<n;i++){
            cin>>p[i].x>>p[i].y;
            p[i].color=0;
            p[i].num=i+1;
        }
        for(int i=n;i<2*n;i++){
            cin>>p[i].x>>p[i].y;
            p[i].color=1;
            p[i].num=i-n+1;
        }
        divide(0,2*n);
        for(int i=1;i<=n;i++)
            cout << ans[i] << endl;
    }
    return 0;
}

然后就可以愉快地AC了！

In The End

UVA1411题：蚂蚁（分治法几何匹配）

题意

分析

代码