分治法：循环日程表问题（从递归到递推）

循环日程表问题

循环日程表问题。n=2k个运动员进行网球循环赛，需要设计比赛日程表。每个选手必须与其他n−1个选手各赛一次；每个选手一天只能赛一次；循环赛一共进行n−1天。按此要求设计一张比赛日程表，该表有n行和n−1列，第i行j列为第i个选手第j天遇到的选手。

得到递归方案

首先这就是我们日常中很容易看到的一个应用问题，向世界杯，或者是足球的各国联赛，还有NBA等等，肯定得把谁跟谁打排好，总不能乱打的吧。所以我们做这道题最好的方法就是找一张这种模型看一看，那么就有了下图。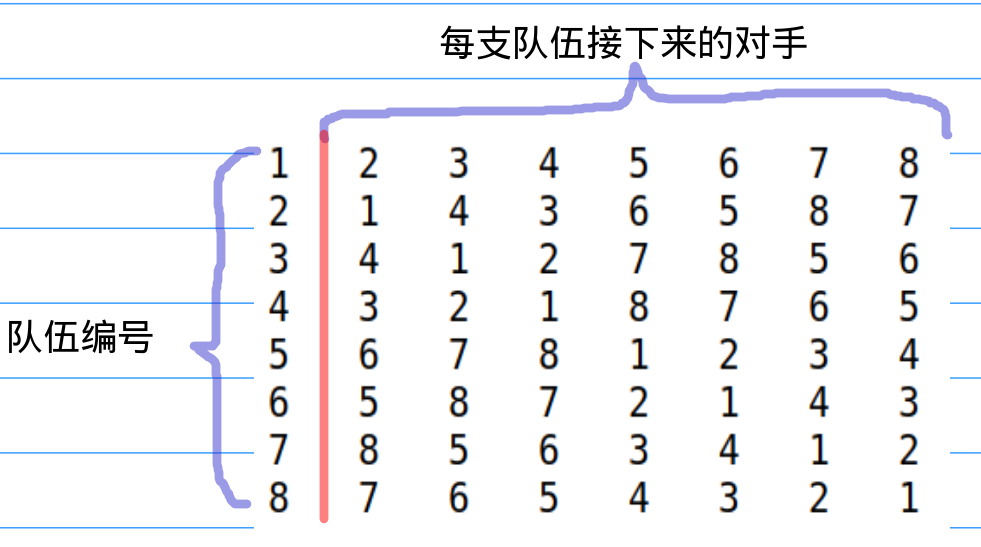

如果不仔细看是肯定看不出名堂的，而且还会眼花缭乱，那，我们再看下一张图。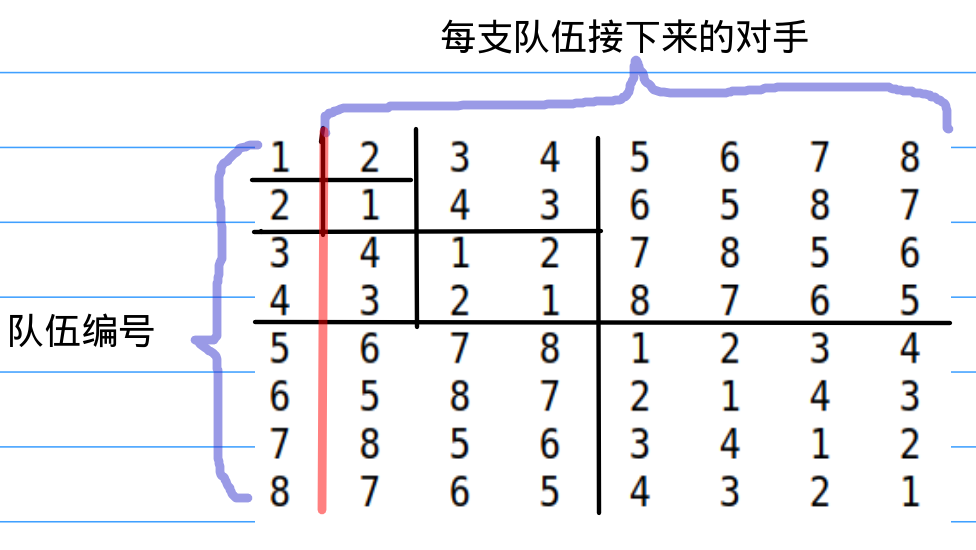

这下还没有看出端倪来吗？没错，右下角的数据都是照搬左上角的，左下角和右上角的数据都是一样的而且是左上角的数据加上边长的一半。

这下会有很多人想到使用递归算法做，类似归并排序一样，先分割再通过左上角的数据进行合并。类似下图一样。下图的红色线是分割的，蓝色线是合并的。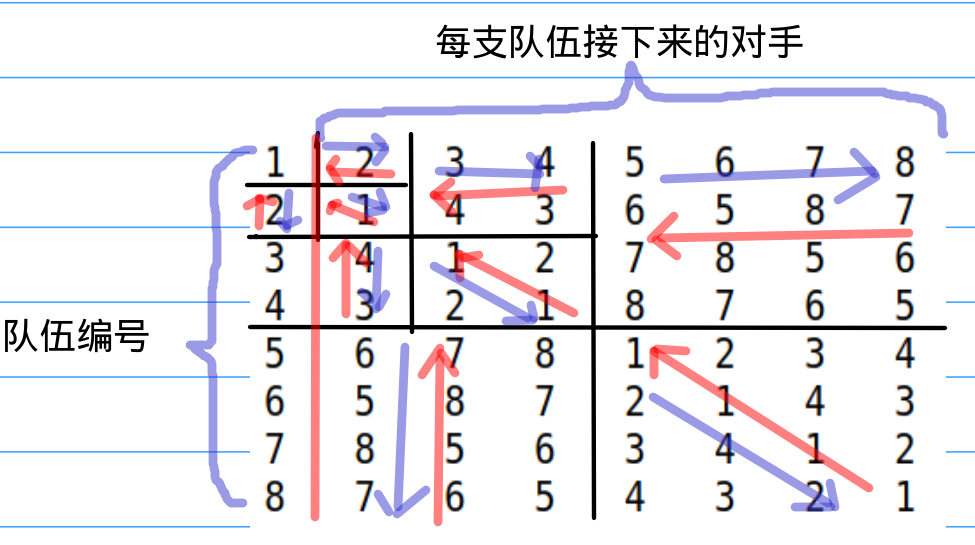

这个方法当然未尝不可，但是对于这样一个已经可以知道所有答案的起源的题目，我们为什么不直接从最左上角出发呢？然后你会惊讶地发现，原来红线根本不需要啊，直接将这个递归的程序变成递推不就行了

从递归到递推

然后我们就可以将图示转化成一个方向的递推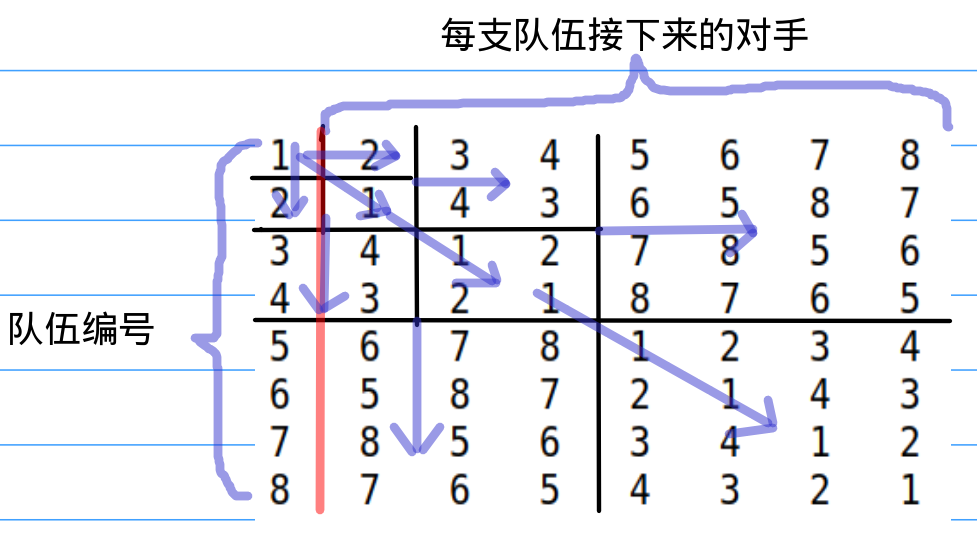

这样我们就能把这个问题完美地解决了

代码

#include <iostream>
#include <cstring>
using namespace std;

int a[1024][1024];

int main(){
    int k;
    while(cin>>k){
        memset(a,0,sizeof(a));
        a[0][0]=1;
        for(int i=0;i<k;i++){
            int len=2<<i;
            int mid=len>>1;
            for(int j=0;j<mid;j++) {
                for (int k = 0; k < mid; k++) {
                    a[j + mid][k] = a[j][k + mid] = a[j][k] + mid;
                    a[j+mid][k+mid]=a[j][k];
                }
            }
        }
        for(int i=0;i<(1<<k);i++){
            for(int j=0;j<(1<<k);j++){
                if(j)
                    cout << '\t';
                cout << a[i][j];
            }
            cout << endl;
        }
    }
}