In The End

个人博客

0%

分治法：棋盘覆盖问题

发表于 更新于 分类于

今天要描述的问题叫做棋盘覆盖问题，这个问题可以很好的利用分治思想解决。

棋盘覆盖

在一个2^k×2^k 个方格组成的棋盘中，恰有一个方格与是黑色的，其他都是白色的，你的任务是使用三个方格组成的L型方格填满整个区域。黑色方格不能被覆盖，白色方格只能被覆盖一次。下图是L型方格的四种摆放方式

下图是一个k为2的棋盘

我们来分析一下这个问题，首先我们可以想到使用分治解决问题，可以将这一张图向四分图算法一样不停地切成四块，然后如果我们切分到了黑色块所在的位置，切分又正好是四个一组，我们就可以在黑块旁边的三个格子上涂上一种颜色了，这样我们就填充完了一个。

那么，问题来了，那剩下这么多怎么办呢。我们可以这么想，我每次切分出来四个区域，只要黑色块在其中一个区域，我就可以将其他三个区域相互交界的位置都涂上一种颜色，也就是把它们等同于黑块继续递归，也就是下图这个样子。

假设k是2，黑块在（1,1），这是我求出来的答案

1
2
3
4
5
2 1 1
2	2	4	4
2	0	1	4
3	1	1	5
3	3	5	5

代码

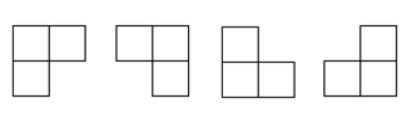
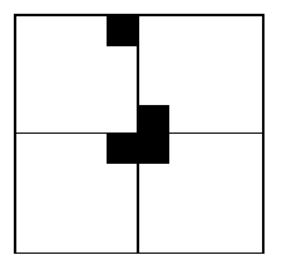
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstring>
using namespace std;
typedef pair<int,int> P;

int a[1024][1024];
int s;

void divide(P u,P v,int len){
    if(len==1)
        return;
    int mid=len/2;
    P np=make_pair(u.first+mid-1,u.second+mid-1);
    if(v.first<=np.first&&v.second<=np.second){
        a[np.first+1][np.second]=a[np.first][np.second+1]=a[np.first+1][np.second+1]=s++;
        divide(u,v,len/2);
        divide(P(u.first+mid,u.second),P(np.first+1,np.second),len/2);
        divide(P(u.first,u.second+mid),P(np.first,np.second+1),len/2);
        divide(P(u.first+mid,u.second+mid),P(np.first+1,np.second+1),len/2);
    }
    if(v.first<=np.first&&v.second>np.second){
        a[np.first][np.second]=a[np.first+1][np.second]=a[np.first+1][np.second+1]=s++;
        divide(u,np,len/2);
        divide(P(u.first+mid,u.second),P(np.first+1,np.second),len/2);
        divide(P(u.first,u.second+mid),v,len/2);
        divide(P(u.first+mid,u.second+mid),P(np.first+1,np.second+1),len/2);
    }
    if(v.first>np.first&&v.second<=np.second){
        a[np.first][np.second]=a[np.first][np.second+1]=a[np.first+1][np.second+1]=s++;
        divide(u,np,len/2);
        divide(P(u.first+mid,u.second),v,len/2);
        divide(P(u.first,u.second+mid),P(np.first,np.second+1),len/2);
        divide(P(u.first+mid,u.second+mid),P(np.first+1,np.second+1),len/2);
    }
    if(v.first>np.first&&v.second>np.second){
        a[np.first][np.second]=a[np.first][np.second+1]=a[np.first+1][np.second]=s++;
        divide(u,np,len/2);
        divide(P(u.first+mid,u.second),P(np.first+1,np.second),len/2);
        divide(P(u.first,u.second+mid),P(np.first,np.second+1),len/2);
        divide(P(u.first+mid,u.second+mid),v,len/2);
    }
}

int main(){
    int k;P start;
    while(cin>>k>>start.first>>start.second){
        memset(a,-1,sizeof(a));
        a[start.first][start.second]=0;
        int len=1;
        for(int i=0;i<k;i++)
            len*=2;
        s=1;
        divide(P(0,0),start,len);
        for(int i=0;i<len;i++){
            for(int j=0;j<len;j++){
                cout << a[i][j] << '\t';
            }
            cout << endl;
        }
    }
    return 0;
}