In The End

个人博客

0%

Binary Search（二分查找）

发表于 更新于 分类于

二分查找

由于后面会有一些使用二分思想的比较灵活的题目，所以我先来写一下二分查找。

首先，二分查找是一个非常基础的算法，也是而二分思想的基础，所以，全面与透彻的了解是非常有必要的。

我们首先假设我们有长度为1000的一个数组，这个数组已经是排好序的了，那么问题来了，我们假设要从这排好序的1000个数字里找一个大小为“100”的数字，我们该怎么找速度最快呢。

首先，最傻的方法莫过于一个一个从头到尾找下去，但是1000个还算撑得住，如果1亿呢？10亿呢？100亿呢？恐怕这个不经推敲的原始算法就扛不住了，这时候我们就要找到一个高效的算法来解决大量数据的问题。

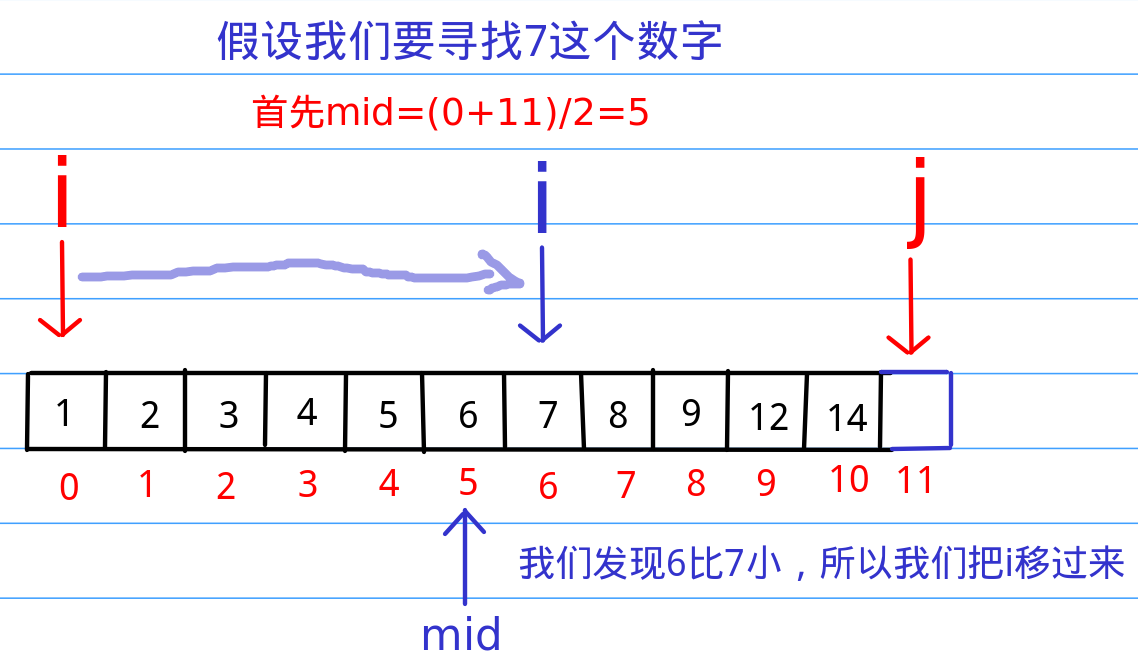
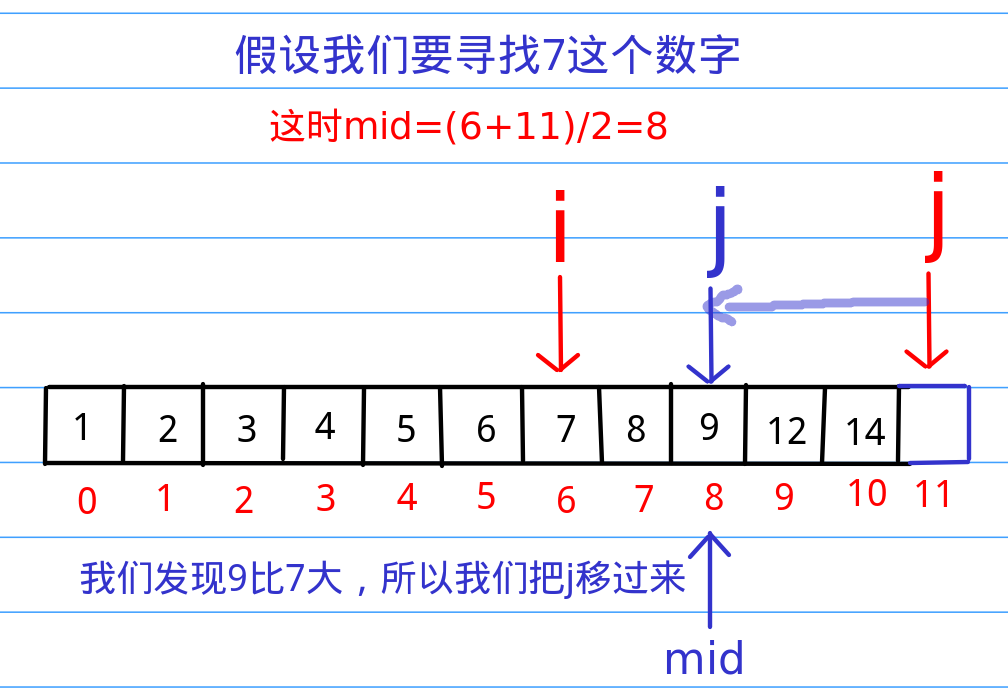
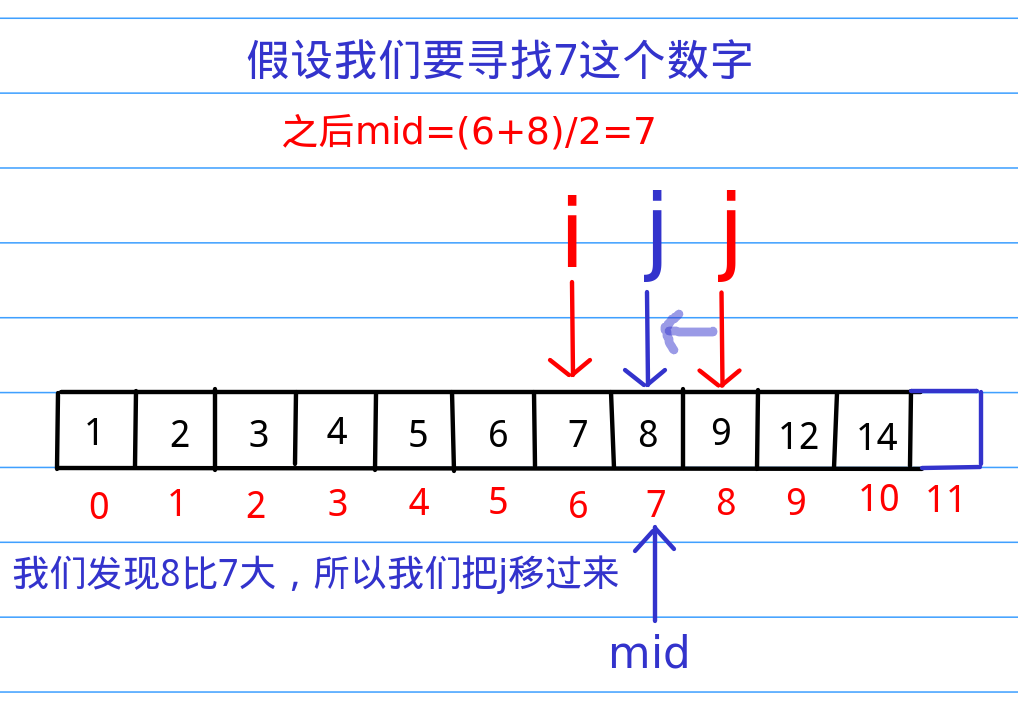
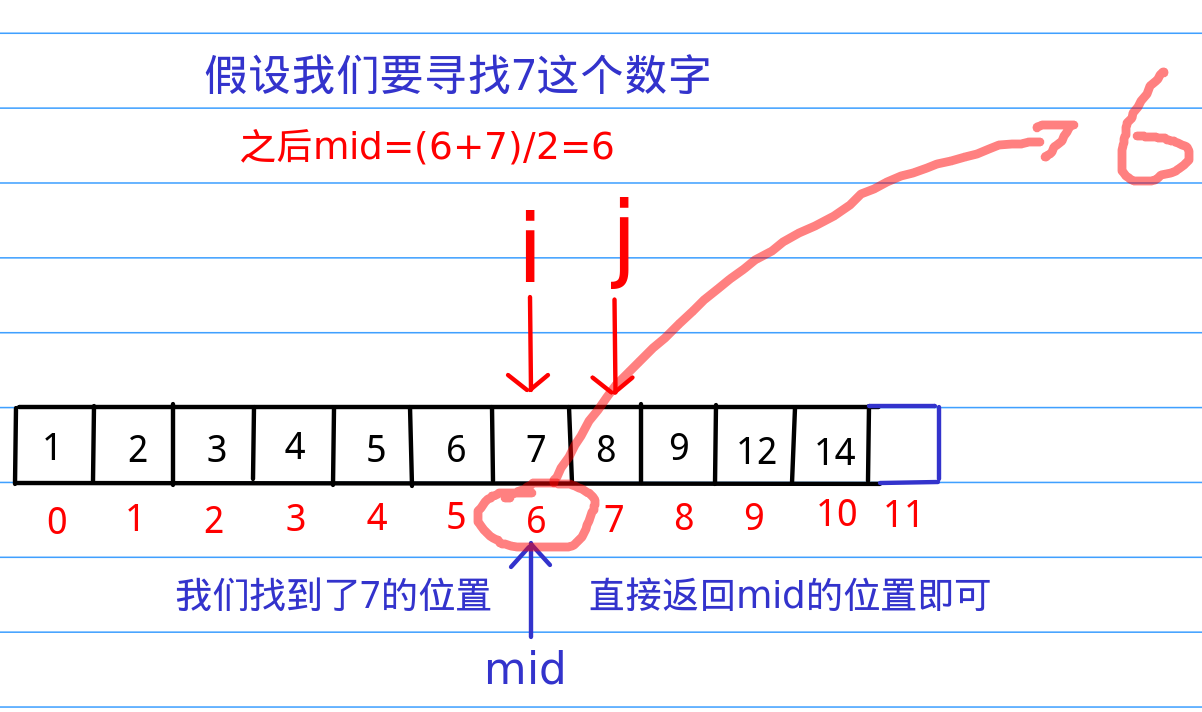
我们可以分析出一个信息，就是刚才那个从头上找下去的算法，完全没有使用数组已经有序这个重要的条件啊！那么，接下来的二分查找就是在数组有序这里找文章（文章：“纳尼？！”）。假设我们在1000个里访问到了第500个，发现第500个数字的大小是20，那么我们可以推断出前500个数字绝对没有大于20的，那么，既然我们的目标是100，傻子都知道前面我们就可以直接忽略了，所以，这种非常高效的排除一大段范围的算法就是二分查找的核心。换点官方的话说就是二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x小于a[n/2],则只要在数组a的左半部分继续搜索x,如果x大于a[n/2],则只要在数组a的右半部搜索x。




二分查找代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
using namespace std;

int binary(int *a,int left,int right,int target){
    int mid;
    while(left<right){
        //mid=(left+right)/2;(溢出漏洞)
        mid=left+(right-left)/2;
        if(a[mid]==target)//查到了
            return mid;//返回位置
        else if(a[mid]<target)//发现答案在更大的地方
            left=mid+1;//把下界往上拉
        else
            right=mid;//反之则把上界向下拉
    }
    return -1;//查不到返回-1
}

int main(){
    int n,target;
    cout << "请输入数组长度:";
    cin>>n;
    int *a=new int[n+10];
    cout << "请输入数组:";
    for(int i=0;i<n;i++)
        cin>>a[i];
    cout << "请输入要查找的数：";
    cin>>target;
    int ans=binary(a,0,n,target);//采用开区间
    if(ans==-1)
        cout << "你查询的数不存在" << endl;
    else
        cout << "你查询的数在数组中下标为" << ans << "的位置" << endl; 
    return 0;
}

查不到就返回下界

当然了，如果应用的时候要使这个查找即使查不到也要返回一个合理的位置。一般都是返回小于你查询值的最后一个位置（因为这样方便添加，你也可以理解为添加的位置），所以我们可以修改上述代码。

二分查找求下界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binary(int *a,int left,int right,int target){
    int mid;
    while(left<right){
        //mid=(left+right)/2;(溢出漏洞)
        mid=left+(right-left)/2;
        if(a[mid]==target)//查到了
            return mid;//返回位置
        else if(a[mid]<target)//发现答案在更大的地方
            left=mid+1;//把下界往上拉
        else
            right=mid;//反之则把上界向下拉
    }
    return left;//查不到返回-1
}

复杂度分析

这个算法的复杂度已经非常清晰了，我们每次都除以2，那么复杂度自然就是O(logn)了

归并与二分的溢出漏洞

这是一个很有趣的事情，以前我也不知道，但是溢出的位置在我今天代码中已经标记了“溢出漏洞”了，大家可以看看，查阅一下资料（顺便提一句，百度百科里的二分查找居然用的是有漏洞的。。。）

关于这个溢出漏洞我可能会写一篇博客，当然也有可能偷懒不写了。