上一篇文章中提到了关于如何使用归并排序求出逆序对的问题,现在是时候揭晓答案了。
其实非常简单,只需要对前面的归并排序添加一个变量,一行代码就可以了,非常的神奇,那么我们来探究一下到底在哪添加代码能快速求出逆序对呢。
首先我们可以分析出来其实逆序对问题跟有序数组排序有很大的关系,为什么呢,我们可以这样思考,想求n个数的逆序对,我们干脆就模仿归并排序。假设有8个数字,我们就分成前四个和后四个,求出前四个数字中比后四个大的个数,这就算出了一部分逆序对,然后我们继续往下切分,我们把前四个数字切成前两个和后两个,然后我们还是像上次一样地去求出前两个之中大于后两个数字的个数,以此类推,当切分完全时,我们通过合并去累加逆序对(实际上前面的比较大小的操作也是在合并中完成的,只不过便于理解我先这样讲),最后我们得到的就是整个数组的逆序对了。
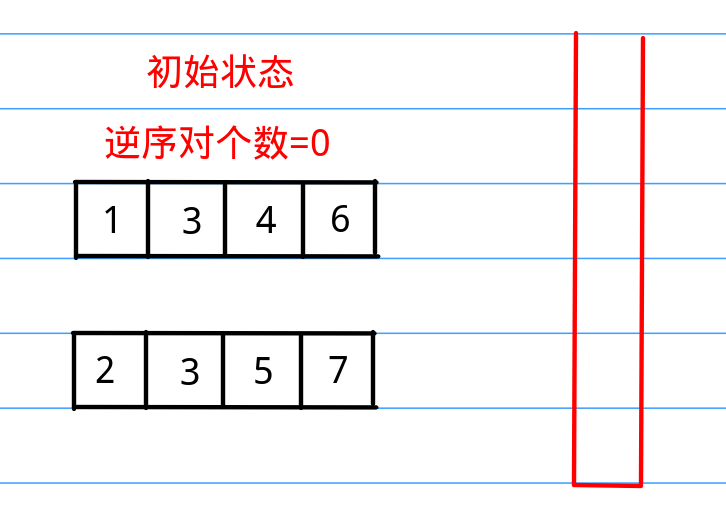

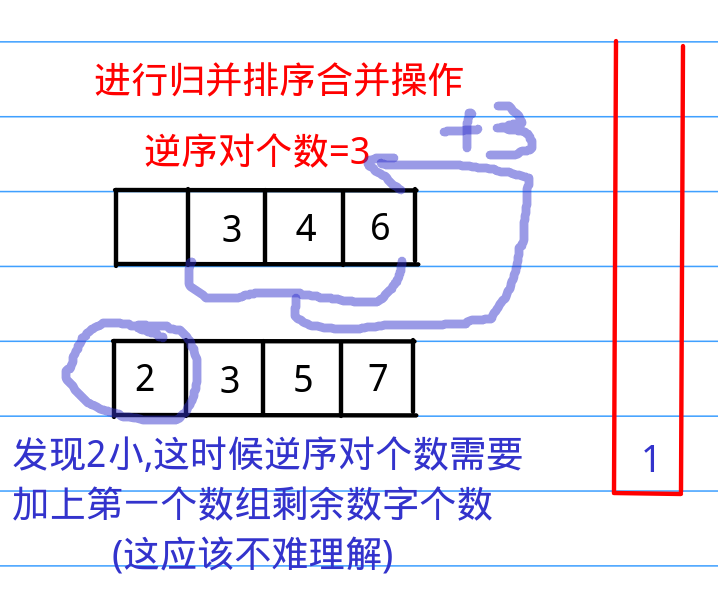
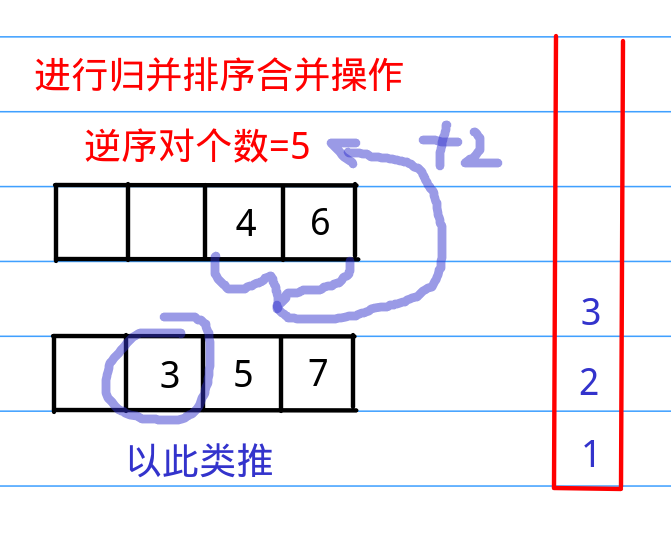
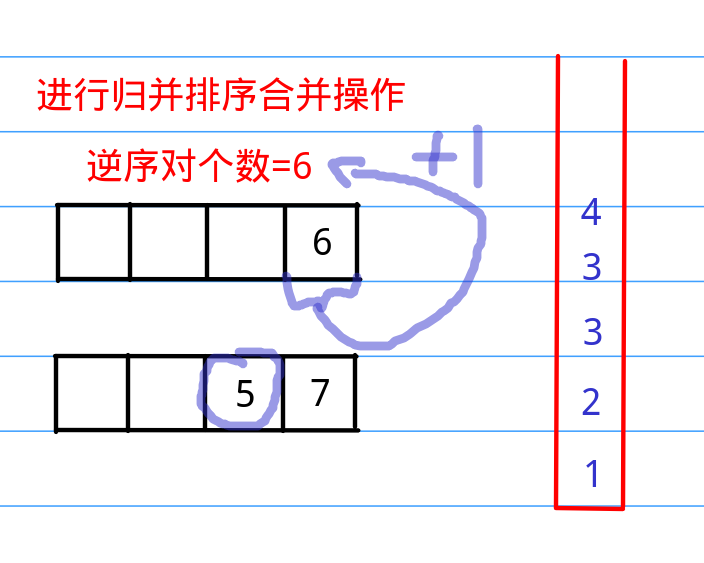

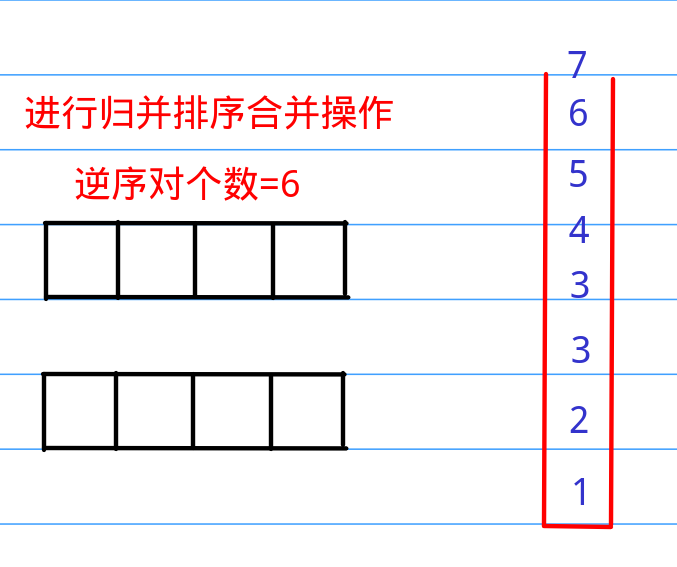
所以,我们只需要在把第二个数组放进新数组的时候统计一下第一个数组中剩余的数字个数,然后添加到总数就可以了。
当然,刚才举例的只是前四个pk后四个,如果我们再计算所有的前两个pk后两个(n=8总共两次),再计算前一个pk后一个(n=8总共四次),我们就可以算出逆序对总数了,这下你明白为什么归并排序可以顺便算出逆序对个数了吧。
好,我们来看代码,代码非常简练,所以要确保你真正理解了上面的步骤。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include <iostream>
using namespace std;
int cnt;
void merge_sort(int *a,int left,int right,int *t){
if(right-left>1){
int mid=left+(right-left)/2;
int p=left,q=mid,i=left;
merge_sort(a,left,mid,t);
merge_sort(a,mid,right,t);
while(p<mid||q<right){
if(q>=right||(p<mid&&a[p]<= a[q]))
t[i++]=a[p++];
else {
t[i++] = a[q++];
cnt+=mid-p;
}
}
for(i=left;i<right;i++)
a[i]=t[i];
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n;
while(cin>>n){
int *a=new int[n+10];
int *t=new int[n+10];
for(int i=0;i<n;i++)
cin>>a[i];
cnt=0;
merge_sort(a,0,n,t);
cout << cnt << endl;
}
return 0;
}
|






