In The End

个人博客

0%

分治法：经典最大连续和问题

发表于 更新于 分类于

最大连续和问题

今天开始写新的一章了，今天要讲的算法就是很常见的分治法了，分治法，顾名思义就是将问题不断分割成子问题然后逐个击破的一种常用算法。

首先来介绍一下今天的题目，今天的题目意思非常简单，我有n个数，需要你编写程序算出哪一个连续区间的数字加起来最大，只需输出最大值就可以了。例如比如有五个数，1,2,3,4,5，那么最大值就是15；又例如五个数为-4,2,3,4,-1，那么就是9为最大值了。当然，在某些特殊情况下一个数也可以变成一个区间。

原始暴力算法

不需要经过太多思考，我们就可以得到一个非常非常直观的方法，那就是枚举所有的区间，然后求出区间和并一直保留最大值，最后等枚举完成后输出最大值，所以我们就会有以下的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n){
        int *a=new int[n+10];
        for(int i=0;i<n;i++)
            cin>>a[i];
        int ans=a[0];
        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                int sum=0;
                for(int k=i;k<=j;k++)
                    sum+=a[k];
                if(sum>ans)
                    ans=sum;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

上面的代码有一点需要注意，就是初始值的问题，我们不能想当然的把初始值设为0，原因非常简单，如果给你的n个数全是负数，你这个初始设置的0就已经把所有区间和都击败了，枚举也就毫无意义，所以我们的初始值设置为第一个区间（也就是数组的第一个数字）

那么，看到中间那一段三个嵌套的for循环，你是不是会有一种不详的预感。对的，像这种看起来似乎并不复杂的题目使用三个for在比赛中估计等着你的就是TLE，我们可以看到如果n变的比较大，不仅是枚举的区间变得非常多，而且每个区间还要用O(len)的时间来求和（len代表区间长度），这消耗非常之大。所以，我们必须要寻找一种足够快速的算法来解决这个问题。

分治法

分治法可以通俗的解释为：把一片领土分解，分解为若干块小部分，然后一块块地占领征服，被分解的可以是不同的政治派别或是其他什么，然后让他们彼此异化。

分治法的精髓：

  • 分—将问题分解为规模更小的子问题；
  • 治—将这些规模更小的子问题逐个击破；
  • 合—将已解决的子问题合并，最终得出“母”问题的解；

在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

“Divide-and-Conquer”，这一个英文词汇就可以很好地概括分治法了，用中文就是“分而治之”，这个算法设计思想其实成为很多更加复杂的算法思想的基础，所以它也是五大常用算法之一（五大常用算法——贪心算法，动态规划算法，分治算法，回溯算法以及分支限界算法）。

在这个最大连续和的问题中，我们使用分治法就可以很好地解决问题，首先，我们对于一个长长的区间（0，n-1），我们先找到中间的点将这个区间切一刀分成两半，最大连续区间顶多只有三种情况：1.在左边的区间里。2.在右边的区间里。3.横跨中间点，是左边区间的右边部分+右边区间的左边部分。三种情况如图所示：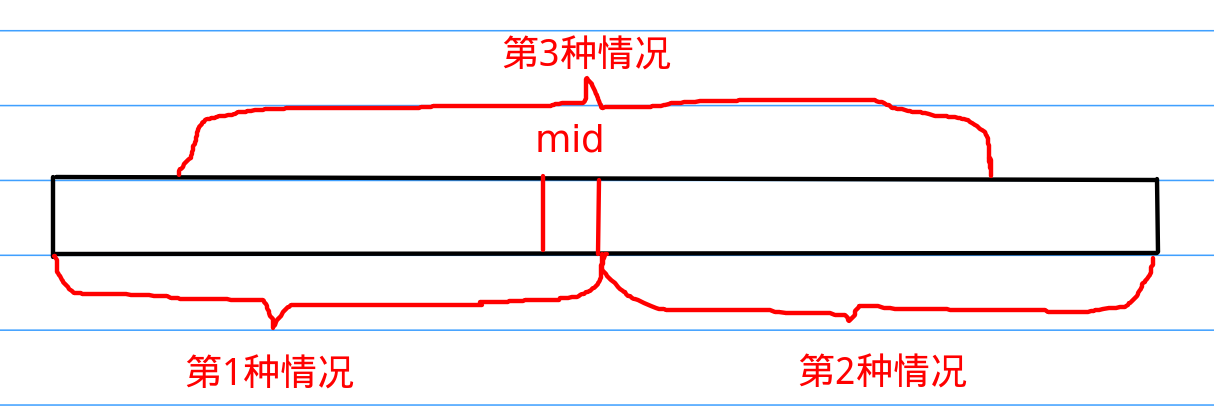

所以，代码就是下面这样子滴

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
using namespace std;

//分治函数，使用了闭区间，left和right为区间内最左和最右的元素
int divide(int *a,int left,int right){
    int L,R,sub,t;
    //处理递归到最深（区间内只有一个元素）的情况
    if(left==right)
        return a[left];
    //处理左右子区间的最大值
    int mid=(left+right)/2;
    //向左右子区间递归，结束后取左右区间的最大值
    sub=max(divide(a,left,mid),divide(a,mid+1,right));
    //处理横跨左右区间的区间最大值
    //往左延伸
    t=0,L=a[mid-1];
    for(int i=mid-1;i>=left;i--)
        L=max(L,t+=a[i]);
    //往右延伸
    t=0,R=a[mid+1];
    for(int i=mid+1;i<=right;i++)
        R=max(R,t+=a[i]);
    //结合两种情况取最大值
    return max(sub,L+R+a[mid])//这里要补上一个a[mid]，因为枚举时没有算进去;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n){
        int *a=new int[n+10];
        for(int i=0;i<n;i++)
            cin>>a[i];
        //因为是闭区间，所以输入0和n-1
        cout << divide(a,0,n-1) << endl;
    }
    return 0;
}

效率分析

然后，我们来就这个代码分析一下为什么分治法会比暴力法快很多。

首先，我们假设解决一个长度为n的区间需要T(n)的时间，那么，我们可以轻松得出计算左边半个和右边半个的时间都为T(n/2)，那么左右的总和就为2*T(n/2)。然后我们再来考虑横跨的情况，横跨的情况我们可以通过程序和图示看出，绝对不会超过n（横跨整个数组正好是n步），所以我们第一分割区间就会得到这个式子T(n)=2*T(n/2)+n,那么，如果我们一直分割下去，由于一直在除以2并加上n，所以，这道题使用分治法的复杂度就是O(nlogn)