In The End

个人博客

0%

分治法：归并排序（多图警告！）

发表于 更新于 分类于

分治法的应用——归并排序

既然我们上一篇讲到了分治法，那么就来提一提由分治法为核心的一个排序算法——归并排序

我上一篇介绍了分治法的一个经典的应用，就是处理最大连续区间和问题，那么，这次这个应用可能更加经典，知道的人也更多，但是，有些人可能并没有将归并排序的核心算法与分治联合起来，虽然他们之间根本就是差不多的。

其实归并排序也就是像前一篇文章中介绍的一样，只需要不停地将排序区间切成两半，不停地切分，但是，与上一个连续区间和问题不同的是，归并排序的合并并不是简单的使用max函数就可以完成的（切分到一个元素的时候可以使用，但是元素数量增多就不行了）。

好，我们现在来正式介绍一下归并排序的原理

首先，请大家考虑这个问题，如果我有两个有序的数组，我该如何将这两个有序数组构造成一个更大的有序数组呢，首先我们需要使用两个指针指向两个数组的最小元素，然后比较，将较小的那个元素拿出来放到新开辟的数组的最开始的位置，然后将指向较小元素的指针向后移动，然后继续比较，以此类推，这样当其中一个指针移动到队尾（说明这个数组已经全部比较完了），我们就把剩下一个指针后面的数字全部移到新数组里去就可以了，这就完成了两个有序数组的合并了，可以看下面的图示：






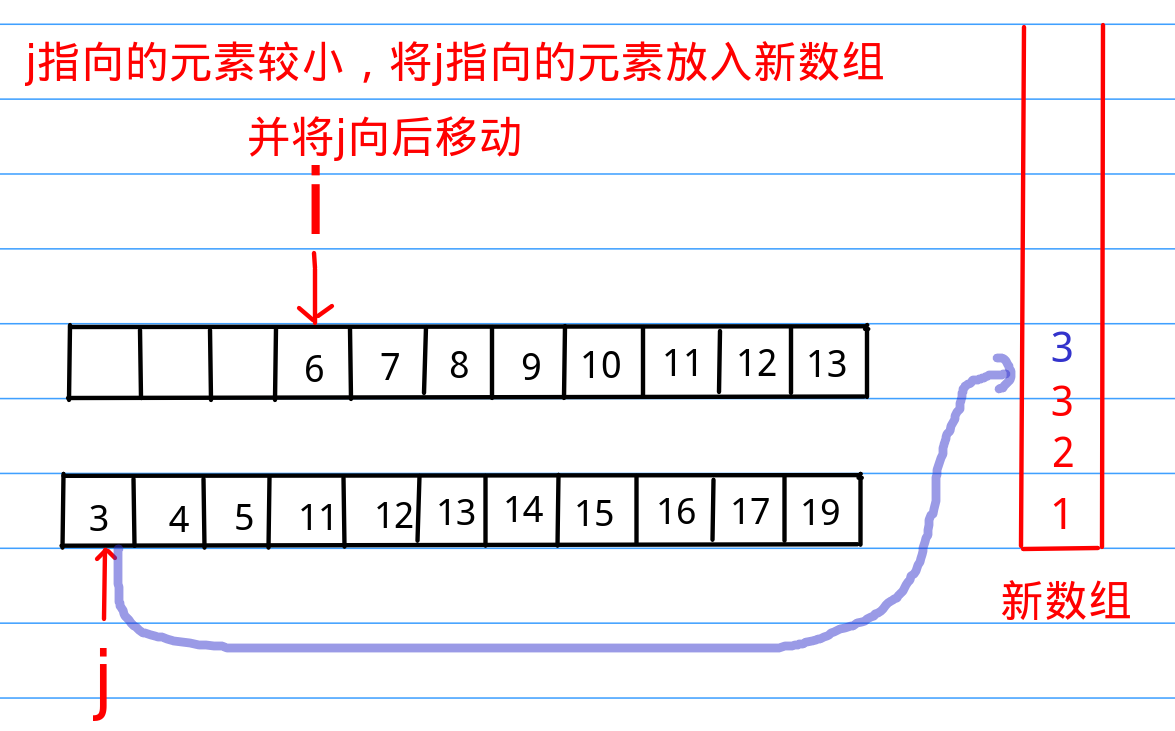
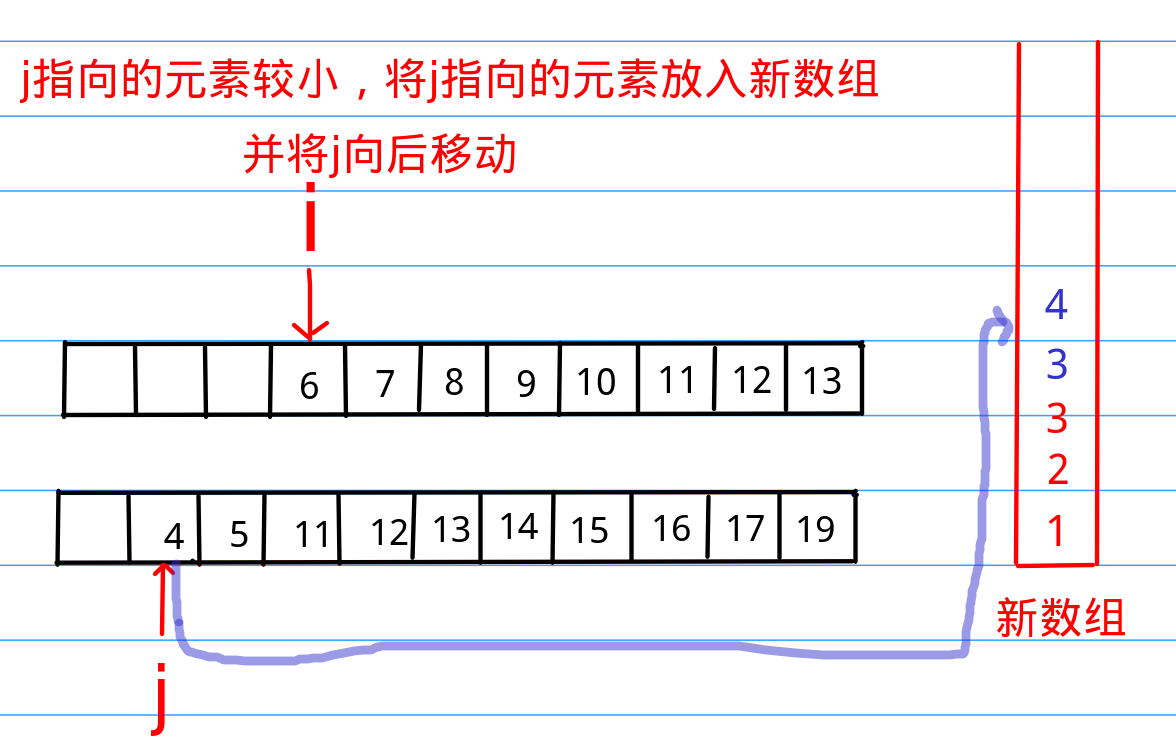
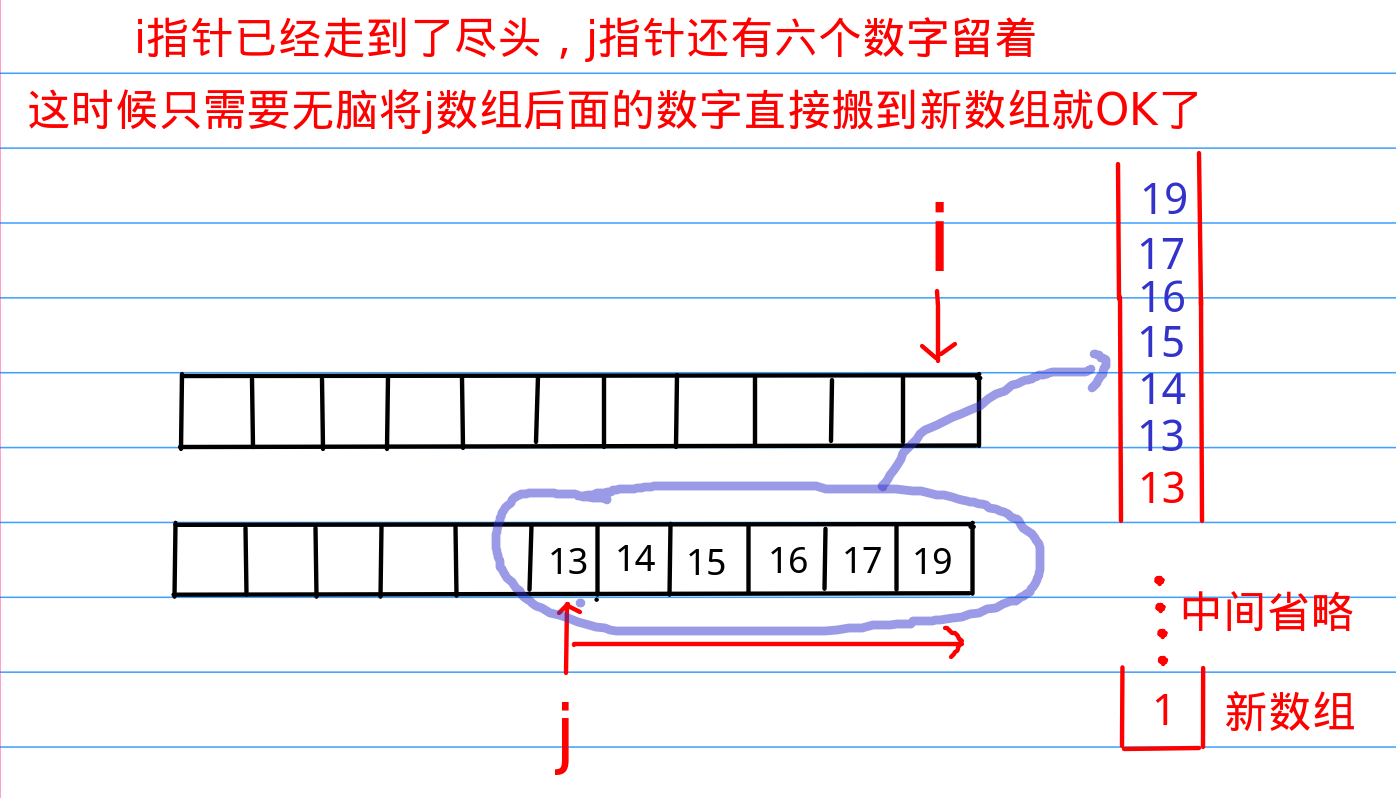
这上面的图可是我一张一张画出来的，是不是对这个过程感觉很清晰了呢？那么我们继续往下走。

我们上面提到的合并过程就是归并排序作为一个分治应用问题所特有的一部分核心操作，可能有些生疏的同学还没有意识到这个合并过程与归并排序的关系。不要紧，我马上就用图示来还原一下归并排序的具体操作，为了清晰明了，我把上面讲的合并过程在下面的途中记为“合并”，当你们看到下面一串图中的“合并”的字时说明是执行上面所说的有序数组合并的过程，ok，下面我放图了：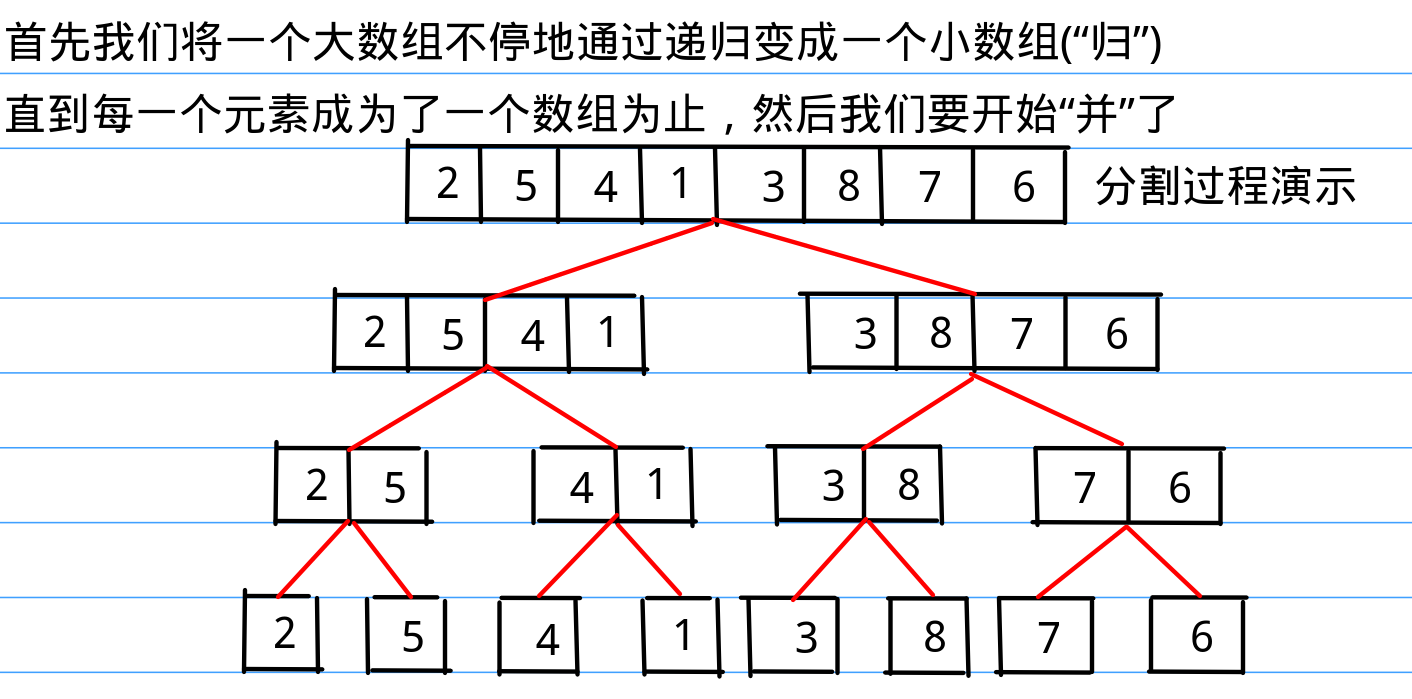




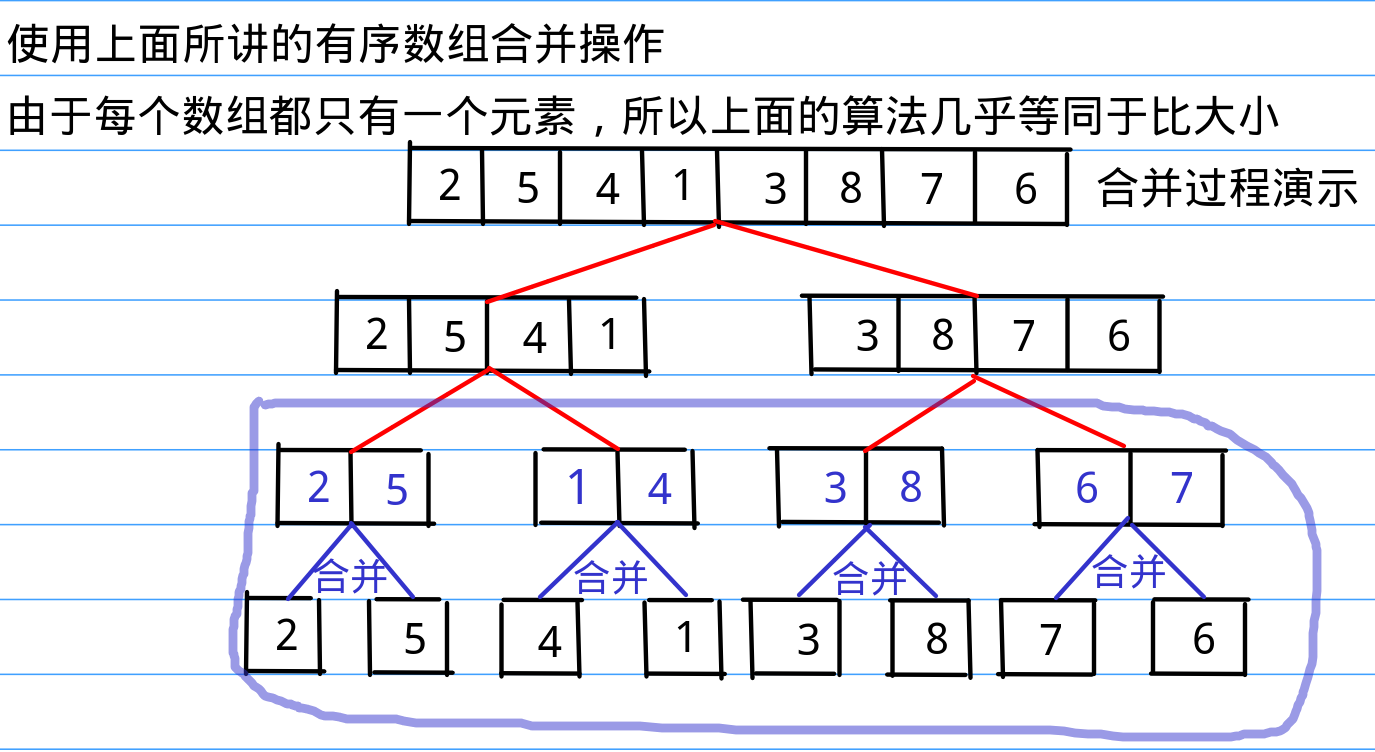
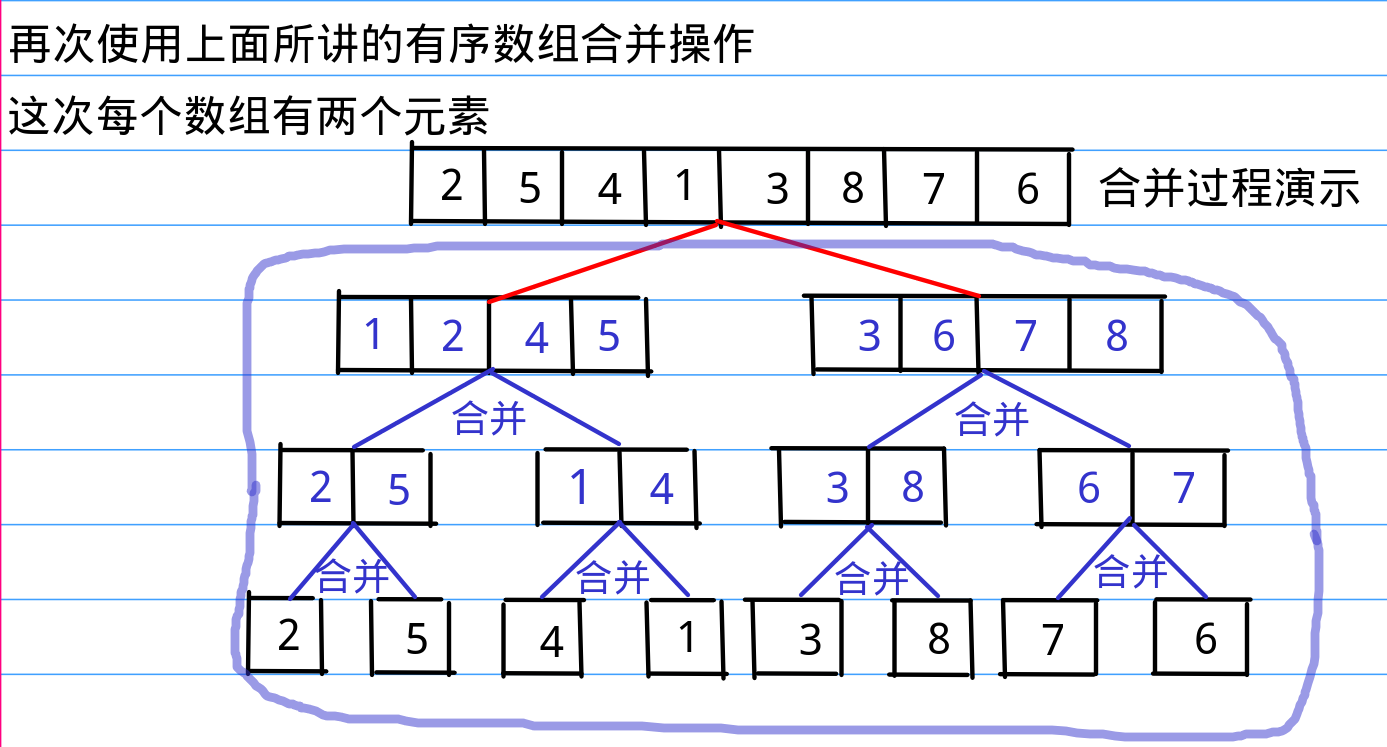
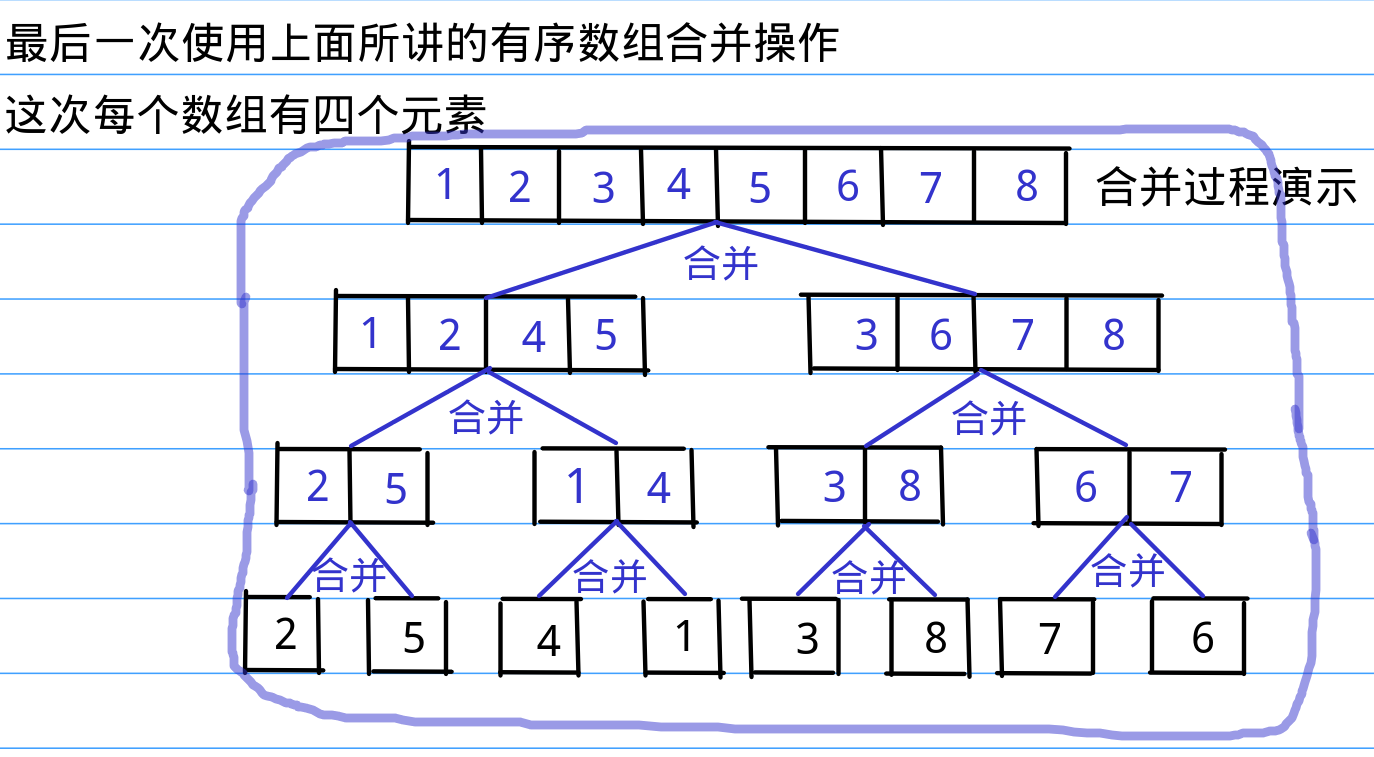
上面图示的过程就是归并排序所有的过程，当然，有人问单数怎么办？其实很简单，有序数组合并操作完全没有要求说两个数组长度必须相等啊，有兴趣试一试的同学可以结合下面的代码自己在脑子里或者纸上走一遍。

趁热打铁！我们来看代码！结合代码你就会完全理解原理了，其实并没有那么难。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
using namespace std;

void merge_sort(int *a,int left,int right,int *t){
    if(right-left>1){//由于一个元素时根本不用操作，所以设立了一个“门槛”
        //int mid=(left+right)/2;(溢出漏洞)
        int mid=left+(right-left)/2;//又是熟悉的配方
        int p=left,q=mid,i=left;
        merge_sort(a,left,mid,t);//左边分割
        merge_sort(a,mid,right,t);//右边分割
        while(p<mid||q<right){//这一个while就是在执行我们的合并操作，你看出来了吗？
            if(q>=right||(p<mid&&a[p]<= a[q]))
                t[i++]=a[p++];
            else
                t[i++]=a[q++];
        }//不妨调试一下或者找张纸模拟一下
        for(i=left;i<right;i++)//重新把排好序的数组还给a
            a[i]=t[i];         // 我的图示中为了直观没有特意画出辅助的t数组，但是在实际操作中是有的
    }
    //如果只有一个元素了就会什么都不做直接从末尾出去
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n){
        int *a=new int[n+10];
        int *t=new int[n+10];
        for(int i=0;i<n;i++)
            cin>>a[i];
        //使用了开区间，归并排序的闭区间算法需要+1-1需要考虑细节过于麻烦，开区间就很方便
        merge_sort(a,0,n,t);
        for(int i=0;i<n;i++){
            if(i) cout << ' ';
            cout << a[i] ;
        }
        cout << endl;
    }
    return 0;
}

时间复杂度

我们上次分析了最大连续区间和问题的时间复杂度，那么今天来分析一下归并排序的，我们几乎可惊讶的发现，两者几乎是相等的，都是O(nlogn)的复杂度，至于怎么推算得来的，大家可以自己研究（很简单），我这里不再赘述。

我这里还有一个问题，那就是我下一篇要写的逆序对问题，我们给出一个由n个数字构成的数组（并没有排好序，乱序的），然后我们要算出里面有多少逆序对。什么是逆序对呢，我举个例子：5,2,1,3,4里面就有五对逆序对：5-2,5-1,5-3,5-4,2-1。

好的，我们怎么才能快速算出逆序对呢，其实非常简单，只需要在归并排的基础上加一点点修改就可以了，希望有兴趣的同学可以自己思考一下，下次我就会写这个问题。

ok，这次归并排序做的非常用心了，感谢大家支持