今天来介绍一下一个比较简单的数据结构——并查集。

介绍

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

在什么情况下我们需要使用并查集呢，这里给出网上一张有趣的图片，非常适合并查集的应用场景。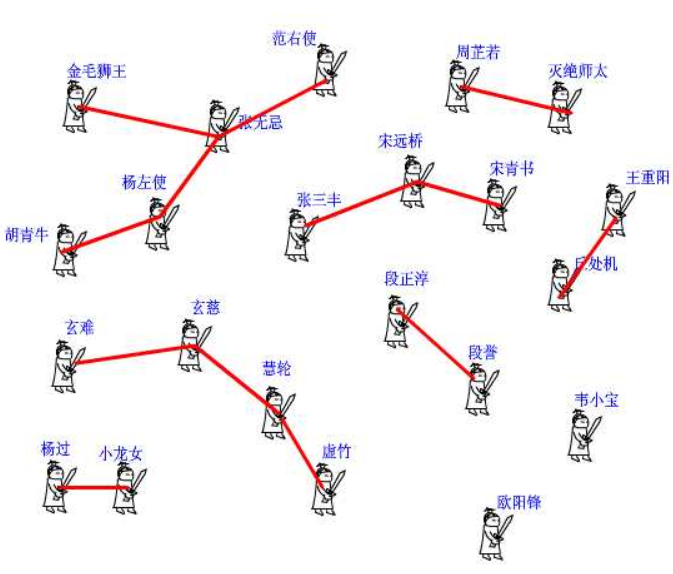

我们可以看到有很多条线连接了许多人物，也可以从这些线中看出来各个势力（被连接的一群人组成），那么我们如何快速地知道这个人所在的是哪个门派哪个势力的，并且还要对这个人进行加入某个门派，又或者是某个门派把另一个门派合并了等等操作，我们就需要使用并查集来快速地解决问题了。

让我来简单地介绍一下并查集，首先并查集并不是什么高端的结构，没有用什么复杂的编程语法，说到底它只是好几棵树而已。首先，并查集的最初都是一个一个离散的点，相互没有关联，就如下图的十个小球一样。

然后我们对其进行操作比如我们这时候发现了小球1和小球7有联系，我们合并1和7，那么我们将小球1作为根，小球7作为子节点，这样，一棵小树就诞生了。

我们继续操作，比如我们又想要合并9和10，我们可以将10作为根，连接9和10,随后3和6都跟4需要合并，我们将4作为根（根的选择没什么规定，随意就行），链接3和4,6和4。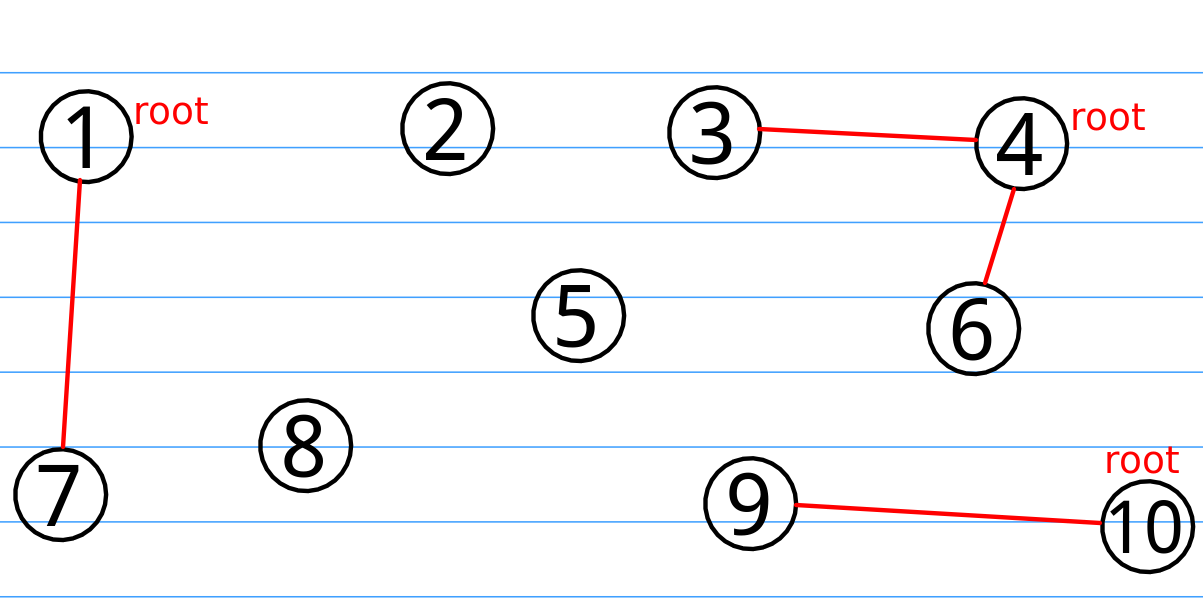

好的，我们就算关系已经全部操作完了，我们现在的程序跑着跑着，需要合并{4,3,6}和{5}这两个集合，所以，我们首先计算一下两个集合哪个深度更大，毫无疑问是{4,3,6}更深，所以，我们将5添加进{4，3,6}。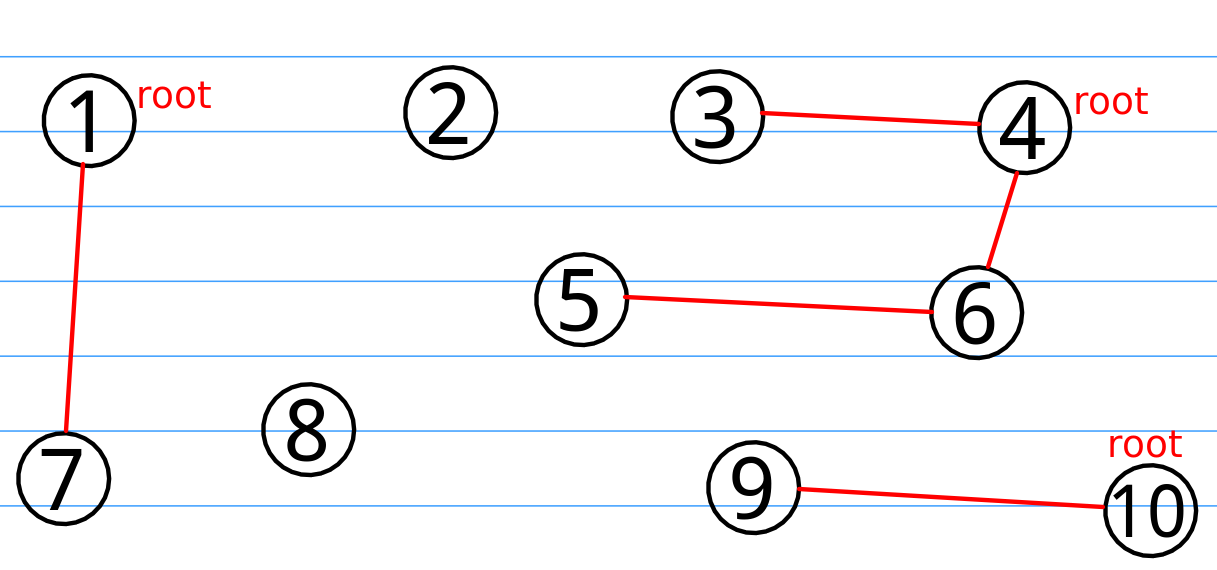

最后我们想合并两个集合，就是{1,7}和{3,4,5,6}，明显，经过深度的比较过后我们需要将{1,7}插入{3,4,5,6}中，最后这个并查集就变成了这个样子。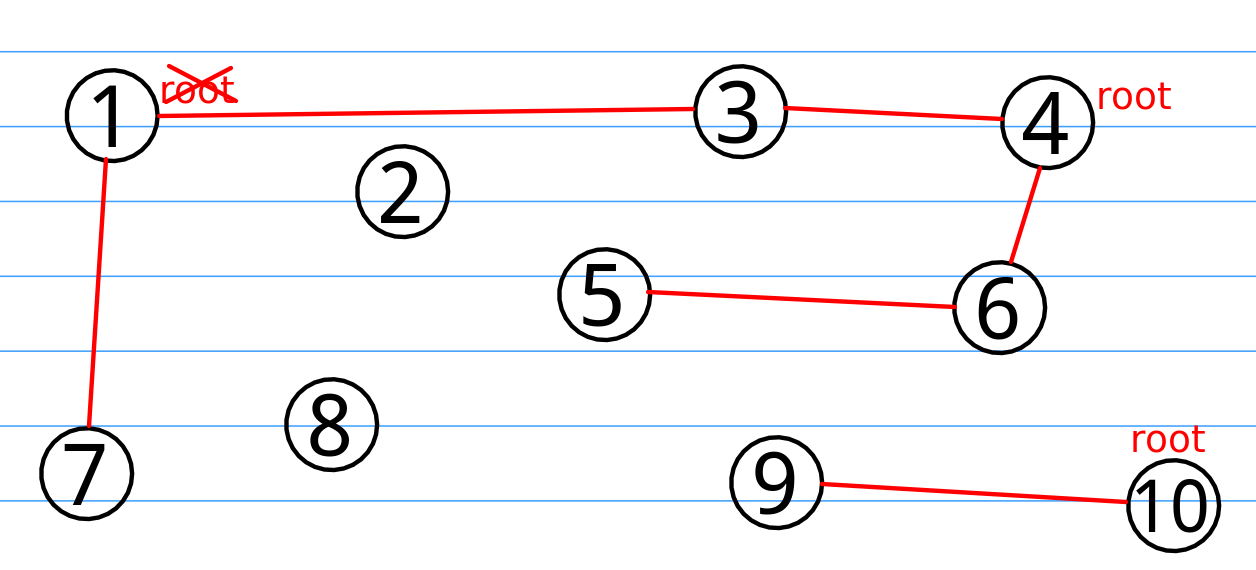

我们可以注意到小球1不再是root了。

假设我们做完了所有的合并操作，那么当我们的程序查询：“1和6是不是在同一个集合内？”，我们可以通过红色的线向上寻找根，我们可以发现两者的root节点都是小球4，所以得出结论两者在一个集合内。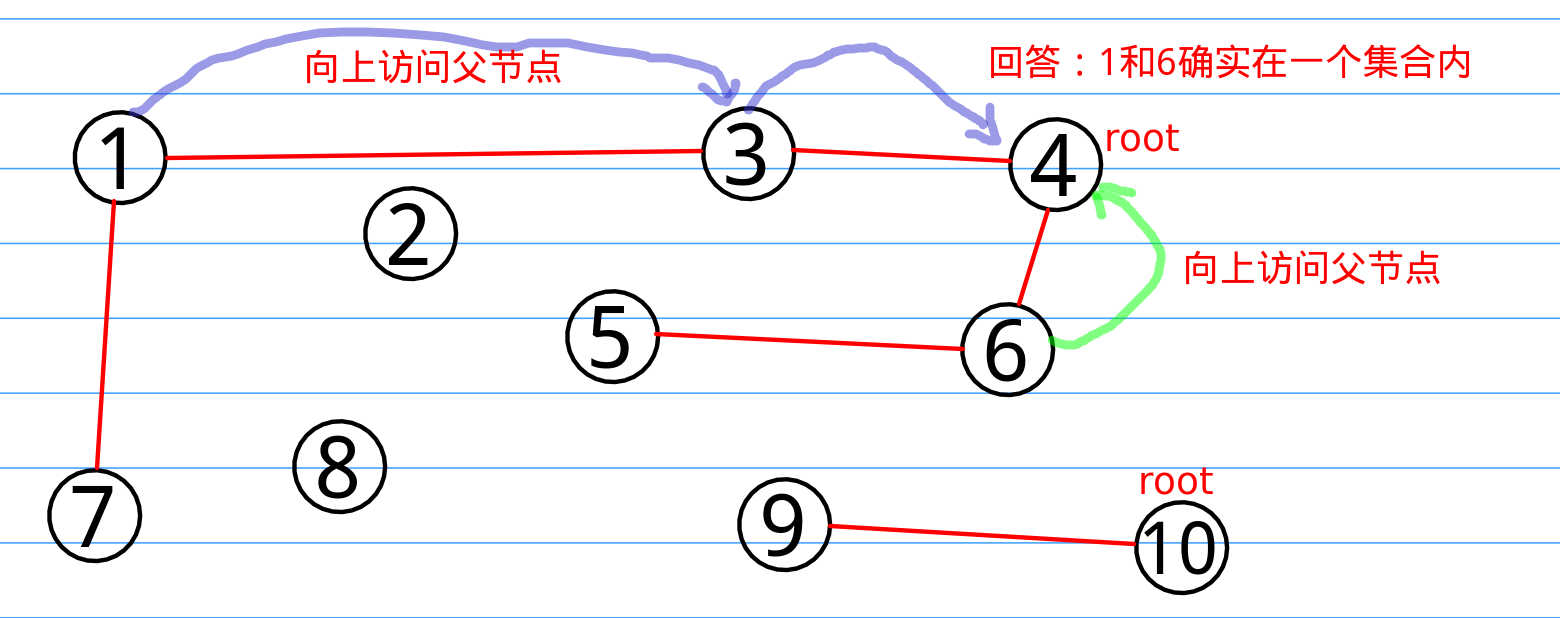

再举一个例子，我们问5和9在不在一个集合内，同样的，我们从5和9开始往上寻找root，却发现两者的root节点不一样，一个是4,一个是10,我们便可以回答，不在一个集合内。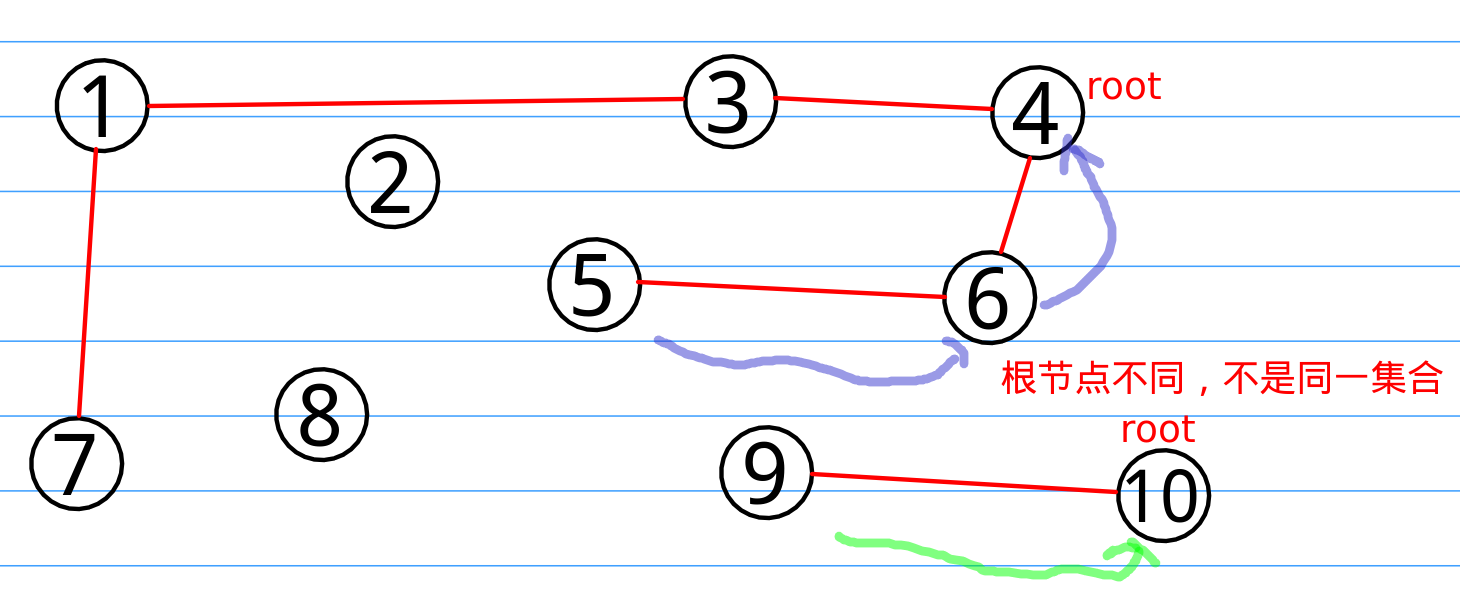

我们再来看看并查集的构造，想要组成并查集，只需要两个一维数组就够了，一个数组记录上级节点，一个数组记录到根节点的距离。初始化时将所有节点的父节点设置成自己，当合并时就把父节点设置为另一个合并的节点，这样会有一个父节点是自己的节点仍然保留着，我们就将其作为根节点，当然，根节点不是一成不变的，就如上图合并中的小球4,当并入其他的集合是会剥夺它当根节点的资格。

代码

int far[25],ran[25];//记录父节点与深度

void init(){//初始化函数
    for(int i=0;i<25;i++){
        far[i]=i;//初始化时将每个点的父节点设置成自己
    }
}
int find(int v){//递归寻找根节点，直到找到父节点是自己的点就是根节点
    return far[v]=far[v]==v?v:find(far[v]);
}
void merge(int x,int y){//合并操作，当深度相等时需要+1深度，这个可以自己画图思考一下为什么
    int a=find(x),b=find(y);
    if(a==b)
        return;
    if(ran[a]<ran[b]){
        far[a]=b;
    }
    else{
        far[b]=a;
        if(ran[a]==ran[b])
            ++ran[a];
    }
}
bool same(int x,int y){//是否在一个集合内
    return find(x)==find(y);
}

好的，为什么现在讲了并查集呢，因为下一题就是关于并查集的应用问题，废话不多说，下一题见。

In The End

数据结构：并查集

介绍

代码