In The End

个人博客

0%

UVA1603题：破坏正方形（IDA*算法）

发表于 更新于 分类于 ，

勤奋的又更新博客了，这次是破坏正方形问题。

题目

首先我们给出题目的传送门：https://vjudge.net/problem/UVA-1603

这道题的大概意思是先给你一个n x n的由火柴组成的大正方形（里面有很多的小正方形），然后题目会将火柴编号，大概就是下图这种顺序：

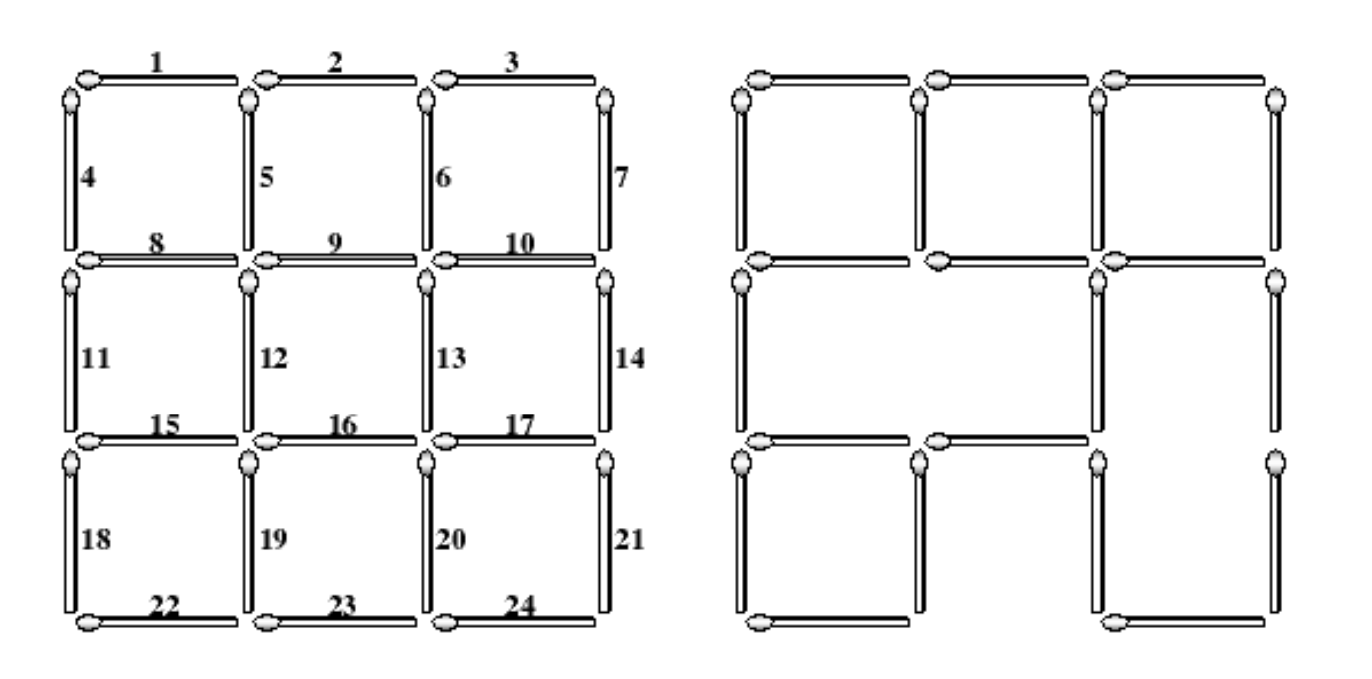
然后题目会给出一组数据，将一些编号的火柴去掉，最后，你需要算出还要去除多少火柴才可以使整个图上没有一个完整的正方形。

首先很明显，我们需要建模，而且，我们可以对去除火柴数进行迭代，所以这又是一道IDA*的题目，既然我们已经确立了大方向，但是如何存储火柴与正方形之间的状态才是这到题目的关键，从方便快捷的角度来看，使用二进制来解决这个问题是一个不错的选择。当然了，我们可以估算一下最大火柴数，如果最大5x5,那么我们就需要60位，这么大的数据int肯定是爆了，幸好，我们还可以使用long long。

具体的方法是，我们使用二进制的一位代表一根火柴，然后我们可以用二进制的与运算符作为添加，异或运算符作为删除，方便的枚举出正方形。我们需要先枚举一遍所有的小正方形，然后在此基础上扩大为大正方形。

最后的任务就是找h(n)函数了，既然他我们是用二进制存储的，那我们就可以很轻松的找到当前状态下还有多少个正方形。所以我们假设每一步我只能破坏掉一个正方形，就可以找到剪枝的办法了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
using namespace std;
typedef long long ll;

int n,m,in,maxd,num;
ll edge[61],small[6][6],big[60];

int up(int x,int y){//上面的火柴
    return (2*n+1)*(x-1)+y;
}
int down(int x,int y){//下面的火柴
    return (2*n+1)*x+y;
}
int left(int x,int y){//左边的火柴
    return (2*n+1)*(x-1)+y+n;
}
int right(int x,int y){//右边的火柴
    return (2*n+1)*(x-1)+y+n+1;
}

bool dfs(int d,ll state){
    if(d==maxd){
        for(int i=1;i<=num;i++)
            if((big[i]&state)==big[i])//是否有完整的正方形
                return false;
        return true;
    }
    int h=0;//还有多少正方形
    ll del=0;//需要删除的正方形
    ll copy=state;
    for(int i=1;i<=num;i++){
        if((big[i]&copy)==big[i]){
            h++;
            copy^=big[i];
            if(!del)//待删除的正方形
                del=big[i];
        }
    }
    if(d+h>maxd)//剪枝
        return false;
    for(int i=1;i<=2*n*(n+1);i++)
        if((del&edge[i])==edge[i])
            if(dfs(d+1,state^edge[i]))//减去一条边，向下一个深度
                return true;
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    edge[1]=1;
    for(int i=2;i<=60;i++)//将每条边用二进制表示
        edge[i]=edge[i-1]<<1;
    int T;
    while(cin>>T){
        while(T--){
            ll state;//状态
            cin>>n>>m;
            state=edge[2*n*(n+1)+1]-1;//首先将所有边填满
            while(m--){
                cin>>in;
                state^=edge[in];//使用异或来删除边
            }
            num=0;//图中总共有多少个正方形
            for(int i=1;i<=n;i++){
                for(int j=1;j<=n;j++){
                    small[i][j]=0;//首先计算小正方形
                    small[i][j]|=(edge[up(i,j)]|edge[down(i,j)]|edge[left(i,j)]|edge[right(i,j)]);
                    big[++num]=small[i][j];//把所有小正方形添加到大正方形中
                }
            }
            for(int i=1;i<n;i++){//添加复合的正方形
                for(int j=1;j+i<=n;j++){
                    for(int k=1;k+i<=n;k++) {
                        big[++num] = 0;
                        for (int x = 0; x <= i; x++)
                            for (int y = 0; y <= i; y++)//向外拓宽
                                big[num] ^= small[j + x][k + y];//使用异或运算来去掉多余的边
                    }
                }
            }
            for(maxd=0;;maxd++){//迭代深度
                if(dfs(0,state))
                    break;
            }
            cout << maxd << endl;
        }
    }
    return 0;
}