题目

有个＃字型的棋盘，2行2列，一共24个格，每个格子上都有一个数字（1或2或3），如下图：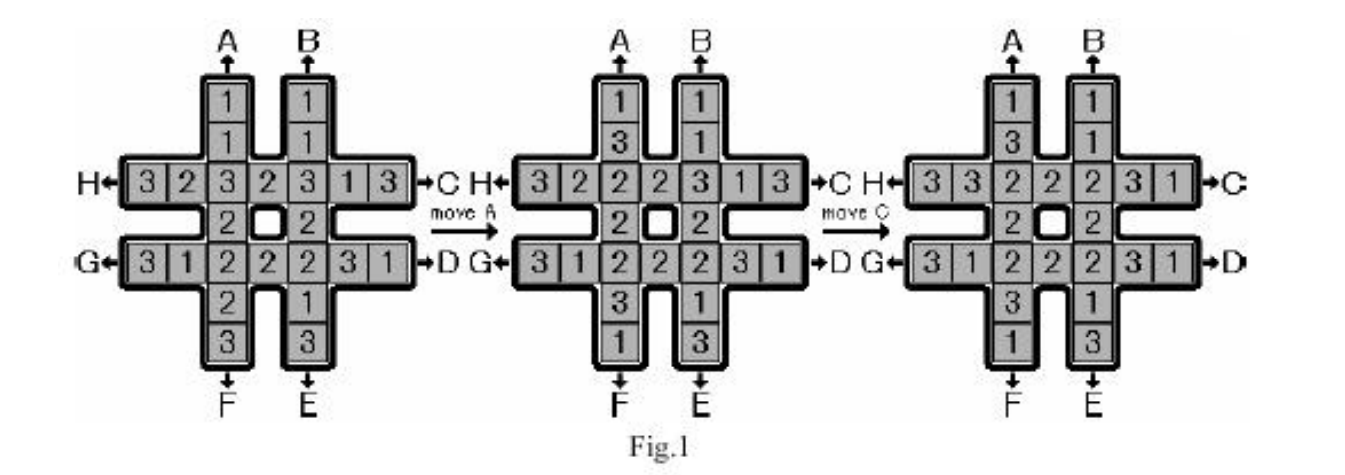

我们可以往A,B,C,D,E,F,G,H八个方向拉动，每次拉动会把离那个字母最靠近的数字移到最远处，然后其他数字会靠近那个字母一位（其实就相当与滚动一样）。现在的目标是找到最短的步数使得中间8个位置的数字相同（要么同时为1,要么同时为2,要么同时为3），如果相同步数有多种情况，则输出字典序最小的那种。

首先我们会想到八数码问题，的确挺像，但是问题在于八数码的情况并没有这个多，如果我们做的操作为x，那我们所得到的情况就为8的x次方，这就非常可怕了，所以这题用BFS做必须要有非常优秀的剪枝。刘老师在书上所写BFS的方法是将1,2,3分开讨论，比如说讨论1的时候将2,3看成同样的数字，这样可以减少枚举情况。

但是，这题并不建议使用BFS，因为非常麻烦，再者，IDA*在解决状态空间问题上可是一个好工具。昨天我们着重介绍了A*算法的g(n)函数和h(n)函数，由于g(n)函数就是深度，所以，我们只需要找到h(n)就能搞定这个问题。

我们可以这样思考，假设每一次我们的移动可以多增加一个相同的数字，那么如果我们最大移动步数（最大深度）减去现在的移动步数无法大于现在仍然所需的相同数字，那我们就可以直接跳出了，所以，我们就得出了h(n)。核心的判断条件为：

d(当前步数)+h()(当前情况下得到答案仍需多少步) < maxn(最大步数)

所以，我们只需对最大步数maxn进行迭代即可

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;

int a[24];
int map[8][7]={//将每个格子对应在一维数组中的位置记下来方便移动
        {0,2,6,11,15,20,22},{1,3,8,12,17,21,23},//A和B
        {10,9,8,7,6,5,4},{19,18,17,16,15,14,13},//C和D
        {23,21,17,12,8,3,1},{22,20,15,11,6,2,0},//E和F
        {13,14,15,16,17,18,19},{4,5,6,7,8,9,10} //G和H
};
//将中心的需要检查的格子在一维数组中的位置记下来
int check[8]={6,7,8,11,12,15,16,17};
int maxd;
char ans[100];

inline int h(){//估计出还要多少步
    int sum1=0,sum2=0,sum3=0;
    for(int i=0;i<8;i++){
        if(a[check[i]]==1)
            sum1++;
        if(a[check[i]]==2)
            sum2++;
        if(a[check[i]]==3)
            sum3++;
    }
    return 8-max(max(sum1,sum2),sum3);
}

void move(int num){//移动
    int t=a[map[num][0]];
    for(int i=1;i<7;i++)
        a[map[num][i-1]]=a[map[num][i]];
    a[map[num][6]]=t;
}

bool dfs(int d){//深度搜索
    int need=h();
    if(!need)
        return true;
    if(d+need>maxd)
        return false;
    int t[24];
    memcpy(t,a, sizeof(a));
    for(int i=0;i<8;i++){
        move(i);
        ans[d]='A'+i;
        if(dfs(d+1))
            return true;
        memcpy(a,t, sizeof(t));
    }
    return false;
}

void sol(){
    if(h()==0){//一开始就正确的情况
        cout << "No moves needed" <<endl;
        cout << a[6] << endl;
        return;
    }
    for(maxd=1;;maxd++){//对最大步数进行迭代
        if(dfs(0)){
            for(int i=0;i<maxd;i++)
                cout << ans[i];
            cout << endl;
            cout << a[6] << endl;
            return;
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    while(cin>>a[0]&&a[0]){
        for(int i=1;i<24;i++)
            cin>>a[i];
        sol();
    }
    return 0;
}

In The End

UVA1343题：旋转游戏（IDA*算法）

题目

代码