In The End

个人博客

0%

UVA11212题：编辑书稿（IDA*算法）

发表于 更新于 分类于 ，

迭代加深搜索 + 启发式搜索（A*） = IDA*

这次所介绍的算法用到了前一篇文章（埃及分数）中介绍过的迭代加深搜索，不熟悉迭代加深搜索的同学建议先看我前一篇文章，介绍IDA*之前，让我们先普及一下A*算法，我后续也会写关于A*算法的题目。

度娘的解释

在一些问题求解时，我们希望能够求解出状态空间搜索的最短路径，也就是用最快的方法求解问题，A*就是干这种事情的！

我们先下个定义，如果一个估价函数可以找出最短的路径，我们称之为可采纳性。A*算法是一个可采纳的最好优先算法。A*算法的估价函数可表示为：

f’(n) = g’(n) + h’(n)

这里，f’(n)是估价函数，g’(n)是起点到节点n的最短路径值，h’(n)是n到目标的最短路经的启发值。由于这个f’(n)其实是无法预先知道的，所以我们用前面的估价函数f(n)做近似。g(n)代替g’(n)，但 g(n)>=g’(n)才可（大多数情况下都是满足的，可以不用考虑），h(n)代替h’(n)，但h(n)<=h’(n)才可（这一点特别的重要）。可以证明应用这样的估价函数是可以找到最短路径的，也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A*算法。

举一个例子，其实广度优先算法就是A*算法的特例。其中g(n)是节点所在的层数，h(n)=0，这种h(n)肯定小于h’(n)。

再说一个问题，就是有关h(n)启发函数的信息性。h(n)的信息性通俗点说其实就是在估计一个节点的值时的约束条件，如果信息越多或约束条件越多则排除的节点就越多，估价函数越好或说这个算法越好。这就是为什么广度优先算法的不甚为好的原因了，因为它的h(n)=0，没有一点启发信息。但在游戏开发中由于实时性的问题，h(n)的信息越多，它的计算量就越大，耗费的时间就越多。就应该适当的减小h(n)的信息，即减小约束条件。但算法的准确性就差了，这里就有一个平衡的问题。

个人理解（通俗易懂）

其实为什么不在前一篇来介绍IDA*算法的目的就在这里，我需要使用前一篇博客的题目（埃及分数问题）的例子，所以没看过埃及分数的同学建议先去补补。在埃及分数问题中，我们只关注两个问题，相加的个数以及分母枚举上限。

接下来为了能让大家更好的理解，我们发动抽象大法，将它看成一个有很多个面组成的空间，每个面上都有一堆金币，而我们是一个淘金者（黄金矿工哈哈），我们必须挖到指定数量的金币才能回家，还有一个关键的条件，越到地底金币越少（挺反常哈）。首先我们从最上面的空间向下深度搜索相加个数相当于挖洞，而在每个面进行枚举分母相当与收集金币，当我们发现的时候我们又继续往下打洞，反复地打洞，找金币，打洞，找金币，直到我们在某一层找到金币为止。

好的，现在你脑子里应该有这么一个景象了，现在我来加深你找宝藏的难度了，如果每一层都非常宽阔或者无限大，你该怎么解决这个问题。这时候你会非常尴尬的觉得这个问题爆炸了靠运气了，好，再给你两个条件，我说假设最大可以挖到maxd层，我给你两个函数，g(n)代表你现在所在的层数，h(n)代表通过你这一层拿到的金币估计接下来你还能挖到多少金币（乐观估价函数）。举个例子吧，假如我让你去一个只能挖三层的地方，挖7个金币，你首先在第一层挖到了三个金币，你非常开心，但是这时候你使用了h(n)大法。

h(n)首先需要g(n)兄弟来帮忙，g(n)兄弟告诉h(n)这里是第一层，h(n)开始计算：恩，第一层挖到了3个么，因为每一层的金币都会比上一层少，所以第二层最多挖出2个，第三层最多挖出一个。然后h(n)跑过来告诉你说你最多还能挖3个金币，然后你就放下铁撬不干了（妈的根本完不成的任务！）。所以，h(n)在这里就相当与一个利用剩余层数快速计算出你接下来会获得的金币的近似值，避免让你白干活。

顺便提一句，许多AI领域或算法研究领域中的路径搜索算法是基于任意(现实情况)的图设计的，而不是基于网格的图。所以，这种依据现实情况“机智”地绕路的算法，非常具有启蒙意义。

我们再给一些例子，这是外国论文中有人测试的例子，同样是有障碍的最短路径，使用BFS与A*相比较
这是基于贪心策略的BFS：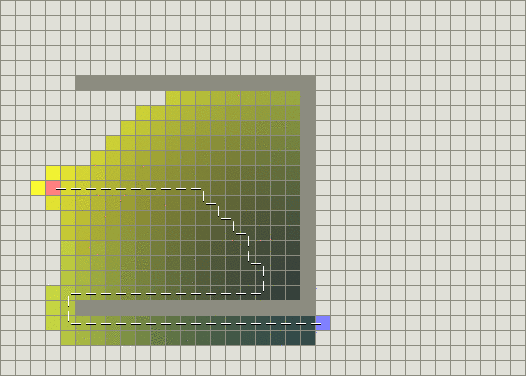

这是曼哈顿距离+A*：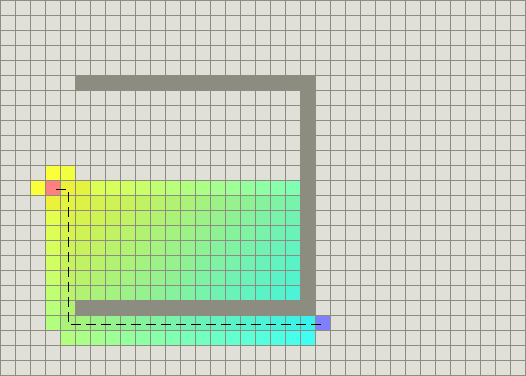

我们可以看到BFS一头撞上了墙，而A*机智地绕开了（了解贪心与BFS的应该会知道为什么会撞墙）。

题意

首先给出传送门https://vjudge.net/problem/UVA-11212

这一次介绍的题目呢也是一道经典的IDA*题目，让我们先看看题意

你有一篇n个自然段组成的文章，希望将它们排列成1，2，…，n。可以用Ctrl+X（剪切）和Ctrl+V（粘贴）快捷键来完成任务。每次可以剪切一段连续的自然段，粘贴时按照顺序粘贴。注意，剪贴板只有一个，所以不能连续剪切两次，只能剪切和粘贴交替。例如，为了将{2，4，1，5，3，6}变为升序，可以剪切1将其放到2前，然后剪切3将其放到4前。再如，排列{3，4，5，1，2}，只需一次剪切和一次粘贴即可——将{3，4，5}放在{1，2}后，或者将{1，2}放在{3，4，5}前。（本段摘自《算法竞赛入门经典（第2版）》）

本题利用迭代加深搜索，可以发现最多只需要n-1步，关键在于如何有效地剪枝。考虑后继不正确的数字的个数h，可以证明每次剪切时h最多减少3（因为一次剪切最多只会改变3个数字的后继，若剪切后这3个数字的后继都正确，则h最多减少了3），因此当h>3*(maxd-d)时剪枝即可，在这里，我们可以不用过于关注哪个是g(n)哪个是h(n)，只要能高效地剪枝就行了

所以我们只需像解决埃及分数问题一样，枚举步数，然后在每一中步数情况中枚举剪切位置即可。

当然我们还可以进行优化，在每次选取剪切的位置的时候，我们不要去选取已经排好序的数字，这样反而会打乱，所以我们只需枚举没有按顺序排的位置。当然，剪切板中的数组最好是有序的，为了整体有序并减少步数，我们应当维持剪切板中的数组也是有序的。

对于这道题与启发式算法的详细解释可以拿这篇博客作为参考：https://blog.csdn.net/flsjzl/article/details/51785488

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

int maxd,n,a[10],b[10];

inline bool judge(){//判断是否已全部有序
    for(int i=1;i<=n;i++)
        if(a[i-1]!=i)
            return false;
    return true;
}

inline int cal(){//计算出还没排好的数字的数量
    int count=0;
    for(int i=1;i<n;i++)
        if(a[i]!=a[i-1]+1)
            count++;
    return count;
}

bool dfs(int d){
    int h=cal();
    if(h==0)
        return true;
    if(3*(maxd-d)<h)
        return false;
    //这里的操作类似于回溯法，所以我们要用copy数组暂时保存a数组，以便枚举完一种情况后回头
    int *copy=new int[n];
    //move数组模拟剪切板
    int *move=new int[n];
    //保存于copy
    memcpy(copy,a, sizeof(int)*n);
    for(int i=0;i<n;i++){//枚举被剪切数组的起点
        if(i==0||a[i]!=a[i-1]+1) {//起点不枚举连续数组的中间部分
            for (int j = i; j < n; j++) {//枚举终点
                while(j!=n-1&&a[j+1]==a[j]+1) j++;//终点枚举连续的数组的末尾
                memcpy(move,copy+i,sizeof(int)*(j-i+1));//将枚举部分放入剪切板
                for(int k=j+1;k<n;k++){//枚举剪切数组插入的位置
                    while(k!=n-1&&a[k+1]==a[k]+1) k++;//同样的，不要破坏已经连续的
                    //移动数组
                    memcpy(a+i,copy+j+1,sizeof(int)*(k-j));
                    memcpy(a+i+k-j,move,sizeof(int)*(j-i+1));
                    //继续向下深搜
                    if(dfs(d+1))
                        return true;
                    //不要忘记回溯回来
                    memcpy(a,copy, sizeof(int)*n);
                }
            }
        }
    }
    return false;
}

int sol(){
    if(cal()==0)
        return 0;
    //枚举最大深度
    for(maxd=1;maxd<n;maxd++){
       if(dfs(0))//从0开始dfs
           return maxd;
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    for(int cas=1;cin>>n&&n;cas++){
        for(int i=0;i<n;i++) {
            cin >> a[i];
        }
        cout <<"Case "<<cas<<": "<< sol() << endl;
    }
    return 0;
}

麻烦的A*与IDA*终于写完了，现在博客能留言了，欢迎大家留言评论！
讲道理挖金币这个例子还是很生动的，毕竟当时灵光一现想出来这么一个例子。
A*与IDA*听起来似乎很高端，其实理解并不难，难点在于应用，找到乐观估价函数等。