In The End

个人博客

0%

埃及分数问题（迭代加深搜索）

发表于 更新于 分类于

问题引入


今天的主题是迭代加深搜索，著名的埃及分数问题（古埃及的智慧。。哈哈)。

我们首先来看问题：
给出一个分数，由分子a 和分母b 构成，现在要你分解成一系列互不相同的单位分数（形如：1/a，即分子为1)，要求：分解成的单位分数数量越少越好，如果数量一样，最小的那个单位分数越大越好。
如：

　　 19/45 = 1/3 + 1/12 + 1/180;

　　 19/45 = 1/5 + 1/6 + 1/18;

以上两种分解方法都要3个单位分数，但下面一个的最小单位分数1/18比上一个1/180大，所以第二个更优。
更多例子：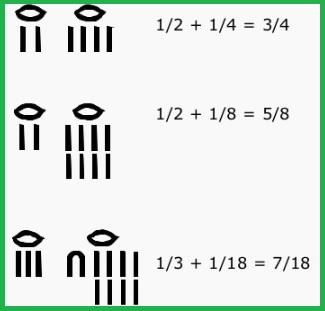

分析

我们如何解决在这个问题呢。首先我们当然会想到枚举分母，可是这可是自然数，根本不可能枚举完所有的情况，还有，相加的个数也枚举不完，完全可以1000个10000个相加甚至更多，所以，普通的搜索根本就束手无策。

我们再思考一下，很明显广搜是死定了（一层不可能搜完），那么改进后的深度搜索说不定可以加上一定的条件来解决这个难题。首先，深搜的深度是1～无穷，那我们就得对其进行优化，每一个分母，都有选中和不选中两种状态，如果选中，那么就减去这个分数，没有就跳过，但是上限究竟在哪呢。我们不妨继续看看题目，题目中特意提到了单位分数数量越少越好，那么，既然多组答案的优先级是由单位分数的个数首先决定，我们和不从2个单位开始，慢慢地放开限制，这次搜两个的，下次搜三个的，下下次搜四个的，ok，看似难办的个数问题就被我们解决了

接下来就是枚举分母的问题了，我们试图从分数的规则去找规律进行剪枝，如果我们无法高效地剪枝耗费的时间仍然会很大。我们可以发现这么一些规律：

1.后面数字的分母一定比前面数字大（不能相同，题目明显指出互不相同）
2.如果假设接下来的分母大小为x，后面的所有数字（总共有几个数字是由上文中枚举个数确定的）的分母都与接下来的分母相等都为x（虽然违反提议，但是你可以把这一步看成是数学课上数列的放缩法），但加起来却没有a/b大，那么我们后面的枚举都没有意义了（再怎么枚举也到不了a/b），所以，这种情况我们就可以剪枝了。

总的来说，我们的大方向就是迭代枚举个数，慢慢地从两个，三个，四个放宽，然后，在具体每一种个数的情况下，我们再去用上文的条件来剪枝，最终我们可以得到理想的答案。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=1000;
ll ans[maxn],v[maxn];
ll a,b;
int cas;
int maxd,ok;

//当一些情况比如2/4我们可以通过同除最大公约数得到1/2，所以需要了gcd函数
ll gcd(ll a,ll b){
    //对gcd不了解的同学可以百度辗转相除法
    return a==0?b:gcd(b%a,a);
}

ll get_first(ll a,ll b){
    //得到接下来一个大于前面分母的数字：i=b/a+1
    return b/a+1;
}

bool better(int d){
    //在枚举个数确定的情况下，只有分母更小的会被采纳
    for(int i=d;i>=0;i--)
        if(v[i]!=ans[i])
            return ans[i]==-1||v[i]<ans[i];
}

bool dfs(int d,ll from,ll a,ll b){
    //如果达到了枚举的上限
    if(d==maxd){
        //测试是否为埃及分数
        if(b%a) return false;
        //将最后一个分母补上
        v[d]=b/a;
        //进入better函数比较答案优先度
        if(better(d))
            //如果v数组的答案更优，则使用内存拷贝，将答案送至ans数组
            memcpy(ans,v, sizeof(ll)*(d+1));
        //递归返回true
        return true;
    }
    bool flag=false;
    //从大于等于前一个分母的数字进行枚举
    from=max(from,get_first(a,b));
    //逐个枚举
    for(int i=from;;i++){
        //如果碰到了(1/i)*(maxd-d+1)<=a/b（即放缩后都无法得到答案）的情况
        //说明已经没有枚举的必要了，所以跳出
        if(a*i>=b*(maxd-d+1))
            break;
        //有必要枚举，则继续深搜，v数组存储答案
        v[d]=i;
        //更新a，b，由式子（（a/b）-（1/i））通分得来
        ll na=a*i-b;
        ll nb=b*i;
        //化简
        ll g=gcd(a,b);
        //同除最大公约数，继续深搜
        if(dfs(d+1,i+1,na/g,nb/g))
            flag=true;
    }
    //递归返回flag
    return flag;
}

void sol(ll a,ll b){
    ok=0;//引入ok标记表示是否成功
    for(maxd=1;;maxd++){//枚举每种个数的情况，设置上限为maxd
        //枚举另一种情况了就清空一遍ans数组
        memset(ans,-1, sizeof(ans));
        //对每一种情况dfs
        if(dfs(0,get_first(a,b),a,b)){
            ok=1;
            break;
        }
    }
    //输出结果
    printf("Case %d: %lld/%lld=",++cas,a,b);
    if(ok){
        for(int i=0;i<maxd;i++)
            printf("1/%lld+",ans[i]);
        printf("1/%lld\n",ans[maxd]);
    }
}

int main(){
    cas=0;
    while(~scanf("%lld%lld",&a,&b))
        sol(a,b);
    return 0;
}

好，埃及分数的问题也解决完了，下一篇见。