真香警告! 这是ACM江湖传说中不做后悔的题! 你还有一秒钟的时间撤离战场! 好,你已经来不及了! 接下来让我们看看今天的主角——八数码问题。
不知道大家小时候有没有玩过这个类似于上图拼图的游戏,我们的目标是要把左边的拼图通过一个空格作为媒介变成右边的拼图的样子(肯定有很多人玩过,但是是通过图片而不是数字,我记得好像windows桌面小工具里就有这个游戏),所以,今天就用计算机来解决这个游戏,输出它的最佳解决方案。 先看看题目吧,POJ1077题,传送门:http://poj.org/problem?id=1077
题意就是输入一个九宫格(字符串),空格用’x’表示,然后我们需要找出把空格怼到最下方且数字还要按顺序排布的移动方案(如图为目标)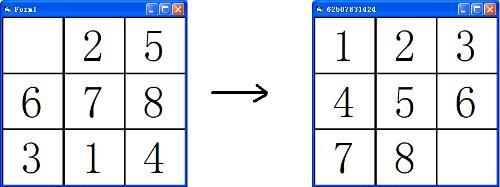
好的废话不多说我们开始分析问题。 首先我们选用BFS来解决这个问题,以空格为起始点,让空格上下左右移动并记录下来,有一个问题是我们需要先解决的,我们得先把x变成数字,那么究竟是变成0还是变成9呢,我这里推荐变成9(我一开始变成0麻烦了一些,不过也不是不行)。为什么要变成9呢?原因就在于康托展开(不熟悉康托展开的同学请易步至我的前一篇博客,这里不再做过多的赘述),在康托展开中,123456789的字典序为0,而123456780的字典序则需要手动调试一次康托展开进行计算(虽然我这里算出来了是46233),所以就比较麻烦,在争分夺秒的环境下推荐直接用123456789,这样心里有底肯定错不了。如图所示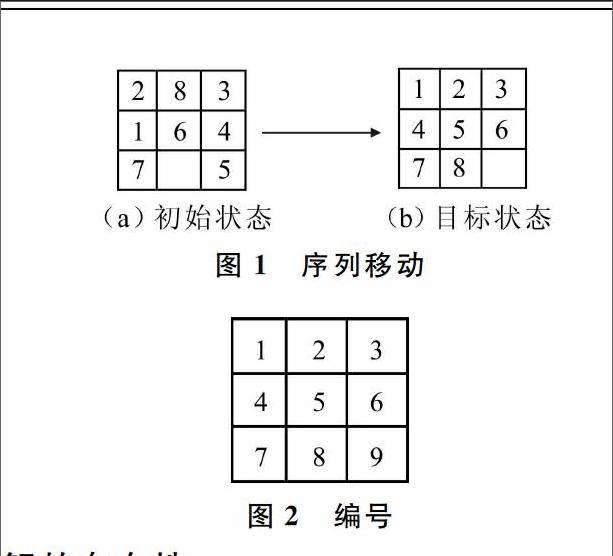
好,然后就是重点了,为什么我们要费尽心机讲了这么多的康托展开,原因就在于,当我们BFS这个八数码的时候,我们怎么去判断这个形态我们已经上一次移动过了(简而言之就是不能走回头路,别移着移着又移回来了),我们开一个9维的vis数组去保存?别逗了!我们直接保存1-9的排列组合不就成了,9!=362880完全ok啊,这就得轮到康托展开大显身手的时候了,所以,在这个问题中我们只需写出康托展开的编码函数与解码函数,然后将BFS的每一步的父节点记下来,最后回溯即可。
给出一张BFS搜索图加深理解: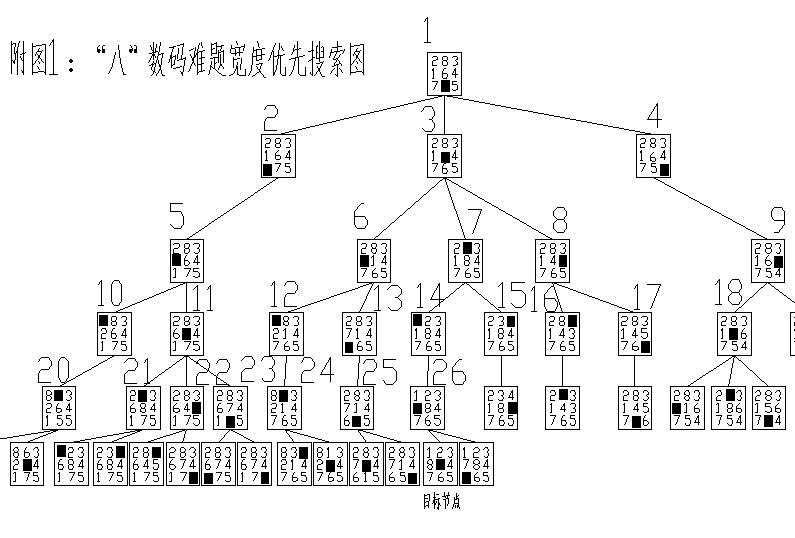
接下来就是AC代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
using namespace std;
const int N = 362880;
int vis[N];
int par[N];
int dir[N];
//这里手动记下了1-9的阶乘,提高效率
const int fact[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};
const int dx[]={-1,1,0,0};
const int dy[]={0,0,-1,1};
struct Node {
char s[9];
int loc;
};
//康托展开编码函数
int encode(const char *a)
{
int i,j,t,sum;
sum=0;
for( i=0; i<9 ;++i)
{
t=0;
for(j=i+1;j<9;++j)
if( a[i]>a[j] )
++t;
sum+=t*fact[9-i-1];
}
return sum+1;
}
//康托展开解码函数
void decode(int k,Node& node) {
int i, j, t, vst[10] = {0};
--k;
for (i = 0; i < 9; i++) {
t = k / fact[9 - i - 1];
for (j = 1; j <= 9; j++)
if (!vst[j]) {
if (t == 0) break;
--t;
}
node.s[i] = j;
vst[j] = 1;
k %= fact[9 - i - 1];
}
for(int i=0;i<9;i++){
if((int)node.s[i]==9){
node.loc=i;
break;
}
}
}
//搜索
void bfs(const Node& begin)
{
memset(vis, 0, sizeof(vis));
int code = encode(begin.s);
vis = 1;
par = -1;//保存了每一步的父节点,便于输出答案
queue<int> que;//BFS标准配置,队列一个,放入康托展开后的编码
que.push(code);
Node n1, n2;
while(!que.empty())
{
int u = que.front();
que.pop();
decode(u, n1);
int k = n1.loc;//loc记下空格所在的位置,方便日后换位
int x = k/3;
int y = k%3;
for(int i=0; i<4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
if(nx>=0 && nx<3 && ny>=0 && ny<3)
{
n2 = n1;
n2.loc = nx * 3 + ny;
swap(n2.s[k], n2.s[n2.loc]);//进行换位你
int v = encode(n2.s);//重新利用康托展开编码
if(!vis[v])
{
dir[v] = i;//保存方向
vis[v] = 1;//表示已经访问
par[v] = u;//记录父节点
if(v==1)
return;
que.push(v);
}
}
}
}
}
void output()
{
int n, u;
char path[1000];
n = 1;
path[0] = dir[1];
u = par[1];
while(par[u]!=-1)
{
path[n] = dir[u];
++n;
u = par[u];
}
for(int i=n-1; i>=0; --i)
{
if(path[i]==0)
cout << "u";
else if(path[i]==1)
cout << "d";
else if(path[i]==2)
cout << "l";
else
cout << "r";
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
Node start;
char c;
for(int i=0; i<9; ++i)
{
cin >> c;
if(c=='x')
{
start.s[i] = 9;//当发现了x,将其变成9
start.loc = i;
}
else
start.s[i] = c - '0';
}
bfs(start);
if(vis[1]==1)
output();
else
cout << "unsolvable";
cout << endl;
return 0;
}
接下来放上一个预告,别以为八数码问题这就解决了,在以后,我还会更新关于八数码的问题,那时候就得用上A*算法(启发式搜索)解决这个问题了。