In The End

个人博客

0%

康托展开（全排列与自然数的双射）

发表于 更新于 分类于

今天来写一个比较简单的算法，叫做康托展开。 算法中使用编码与解码的场景是非常多的（例如我接下来要写的八数码问题），比如，一个九宫格中数字的排布，或者一个字符串字符的排布，如果我们使用map或者set来判定是否重复，是非常耗时的，有可能就会疯狂TLE，那么我们此时就可以选择康托先生发明的算法来用O(1)的时间解决重合的问题。
首先介绍一下，这个人就叫康托，是一位德国的大数学家，主要是研究集合论的，还涉及到了实变函数等高端数学知识（不过这不是我们今天要讨论的)，让我们看看19世纪的康托是怎么解决这个问题的。

康托展开

首先介绍一下康托展开的定义：康托展开是一个全排列到一个自然数的双射，常用于构建hash表时的空间压缩。设有n个数（1，2，3，4,…,n），可以有组成不同(n!种)的排列组合，康托展开表示的就是是当前排列组合在n个不同元素的全排列中的名次。 什么叫做双射呢，就是指双向映射，正好就对应于计算机中的编码与解码。其中的编码映射对应于这样一个公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 我们来解析一下a[n]代表的意思 其中, a[i]为整数，并且0 <= a[i] <= i, 0 <= i < n, 表示当前未出现的的元素中排第几个，这就是康托展开。 例如有3个数（1，2，3），则其排列组合及其相应的康托展开值如下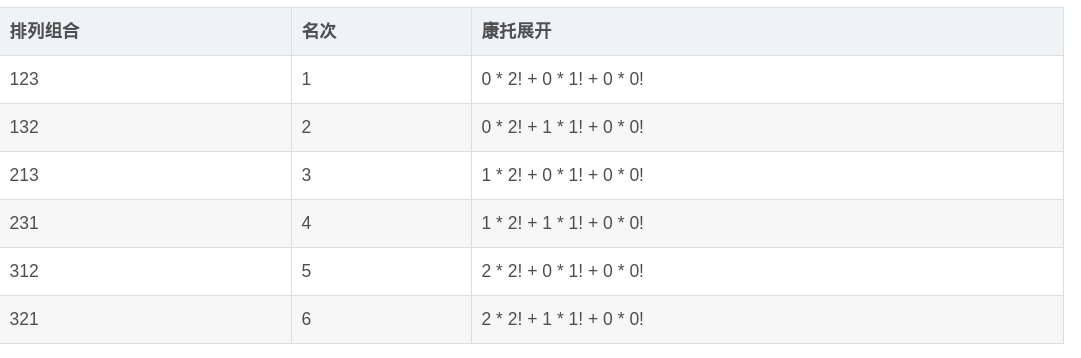： 比如其中的 231：

  • 想要计算排在它前面的排列组合数目（123，132，213），则可以转化为计算算比首位小及小于2的所有排列「1 2！」，首位相等及为2第二位小于3的所有排列「1\1！」，前两位相等及为23第三位小于1的所有排列（0*0！）的和即可，康托展开为：1*2！+1*1+0*0=3。
  • 所以小于231的组合有3个，所以231的名次是4。

再举个例子说明。 在（1，2，3，4，5）5个数的排列组合中，计算 34152的康托展开值。

  • 首位是3，则小于3的数有两个，为1和2，a[5]=2，则首位小于3的所有排列组合为 a[0]*(5-1)!
  • 第二位是4，则小于4的数有两个，为1和2，注意这里3并不能算，因为3已经在第一位，所以其实计算的是在第二位之后小于4的个数。因此a[4]=2
  • 第三位是1，则在其之后小于1的数有0个，所以a[3]=0
  • 第四位是5，则在其之后小于5的数有1个，为2，所以a[2]=1
  • 最后一位就不用计算啦，因为在它之后已经没有数了，所以a[1]固定为0
  • 根据公式： X = 2 * 4! + 2 * 3! + 0 * 2! + 1 * 1! + 0 * 0! = 2 * 24 + 2 * 6 + 1 = 61
  • 所以比 34152 小的组合有61个，即34152是排第62

具体代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int vis[362880];//因为9!=362880所以开辟362880，不放心可以多开几个
int fact[9];//保存0-8的阶乘值，方便计算
void init(){//首先打印出0-8阶乘的值直接保存在fact数组
    memset(vis,0,sizeof(vis));
    fact[0]=1;
    for(int i=1;i<9;i++){
        fact[i]=fact[i-1]*i;//使用前一个数组值快速求阶乘
    }
}
int encode(const char *a)//编码函数
{
    int i,j,t,sum;
    sum=0;
    for( i=0; i<9 ;++i)
    {
        t=0;
        for(j=i+1;j<9;++j)
            if( a[i]>a[j] )
                ++t;
        sum+=t*fact[9-i-1];
    }
    return sum+1;
}

逆康托展开

一开始已经提过了，康托展开是一个全排列到一个自然数的双射，因此是可逆的。即对于上述例子，在（1，2，3，4，5）给出61可以算出起排列组合为 34152。由上述的计算过程可以容易的逆推回来，具体过程如下：

  • 用 61 / 4! = 2余13，说明a[5]=2,说明比首位小的数有2个，所以首位为3。
  • 用 13 / 3! = 2余1，说明a[4]=2，说明在第二位之后小于第二位的数有2个，所以第二位为4。
  • 用 1 / 2! = 0余1，说明a[3]=0，说明在第三位之后没有小于第三位的数，所以第三位为1。
  • 用 1 / 1! = 1余0，说明a[2]=1，说明在第二位之后小于第四位的数有1个，所以第四位为5。
  • 最后一位自然就是剩下的数2啦。
  • 通过以上分析，所求排列组合为 34152。

这里放上一段简洁的逆康托展开的代码(经过测试无误)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void decode(int k,int* node) {
    int i, j, t, vst[10] = {0};
    --k;
    for (i = 0; i < 9; i++) {
        t = k / fact[9 - i - 1];
        for (j = 1; j <= 9; j++)
            if (!vst[j]) {
                if (t == 0) break;
                --t;
            }
        node[i] = j;
        vst[j] = 1;
        k %= fact[9 - i - 1];
    }
}